Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) y' = 4x3 – 4x = 4x(x2 - 1) ; y' = 0 ⇔ 4x(x2 - 1) = 0 ⇔ x = 0, x = 1.
y'' = 12x2 - 4 .
y''(0) = -4 < 0 nên hàm số đạt cực đại tại x = 0, ycđ = y(0) = 1.
y''(1) = 8 > 0 nên hàm số đạt cực tiểu tại x =
1, yct = y(
1) = 0.
b) y' = 2cos2x - 1 ;
y'' = -4sin2x .
nên hàm số đạt cực đại tại các điểm x =
+ kπ, ycđ = sin(
+ k2π) -
- kπ =
- kπ , k ∈ Z.
nên hàm số đạt cực tiểu tại các điểm x =
+ kπ, yct = sin(
+ k2π) +
- kπ =
- kπ , k ∈ Z.
c) y = sinx + cosx = ; y' =
;
![]()
Do đó hàm số đạt cực đại tại các điểm , đạt cực tiểu tại các điểm
d) y' = 5x4 - 3x2 - 2 = (x2 - 1)(5x2 + 2) ; y' = 0 ⇔ x2 - 1 = 0 ⇔ x = ±1.
y'' = 20x3 - 6x.
y''(1) = 14 > 0 nên hàm số đạt cực tiểu tại x = 1, yct = y(1) = -1.
y''(-1) = -14 < 0 hàm số đạt cực đại tại x = -1, ycđ = y(-1) = 3.

a) y' = 4x3 – 4x = 4x(x2 - 1) ; y' = 0 ⇔ 4x(x2 - 1) = 0 ⇔ x = 0, x = 1.
y'' = 12x2 - 4 .
y''(0) = -4 < 0 nên hàm số đạt cực đại tại x = 0, ycđ = y(0) = 1.
y''(1) = 8 > 0 nên hàm số đạt cực tiểu tại x =
1, yct = y(
1) = 0.
b) y' = 2cos2x - 1 ;
y'' = -4sin2x .
nên hàm số đạt cực đại tại các điểm x =
+ kπ, ycđ = sin(
+ k2π) -
- kπ =
- kπ , k ∈ Z.
nên hàm số đạt cực tiểu tại các điểm x =
+ kπ, yct = sin(
+ k2π) +
- kπ =
- kπ , k ∈ Z.
c) y = sinx + cosx = ; y' =
;
![]()
Do đó hàm số đạt cực đại tại các điểm , đạt cực tiểu tại các điểm
d) y' = 5x4 - 3x2 - 2 = (x2 - 1)(5x2 + 2) ; y' = 0 ⇔ x2 - 1 = 0 ⇔ x = ±1.
y'' = 20x3 - 6x.
y''(1) = 14 > 0 nên hàm số đạt cực tiểu tại x = 1, yct = y(1) = -1.
y''(-1) = -14 < 0 hàm số đạt cực đại tại x = -1, ycđ = y(-1) = 3.

y’ = 3x2 – 2mx – 2 , ∆’ = m2 + 6 > 0 nên y’ = 0 có hai nghiệm phân biệt và y’ đổi dấu khi qua các nghiệm đó.
Vậy hàm số luôn có một cực đại và một cực tiểu.


a) 2x2 + x - 18 chia hết cho x - 3
\(\Rightarrow\) (2x . x) + x - 18 chia hết cho x - 3
\(\Rightarrow\) 3x + x - 18 chia hết cho x - 3
\(\Rightarrow\) 4x - 18 chia hết cho x - 3
\(\Rightarrow\) 4x - 12 - 6 chia hết cho x - 3
\(\Rightarrow\) 4(x - 3) - 6 chia hết cho x - 3
\(\Rightarrow\) (-6) chia hết cho x - 3
\(\Rightarrow\) x - 3 \(\in\) Ư(-6) = {-1; -2; -3; -6}
\(\Rightarrow\) x \(\in\) {2; 1; 0; -3}
b) 25 - y2 = 8(x - 2013)2
25 - y . y = 8(x - 2013)(x - 2013)
25 - 2y = 8 - 2(x - 2013)
25 - 2y = 8 - (2x - 2 . 2013)
25 - 2y = 8 - (2x - 4026)
25 - 2y = 8 - 2x + 4026
25 - 2y = (8 + 4026) - 2x
25 - 2y = 4034 - 2x
a) 2x2 + x - 18 chia hết cho x - 3
\(\Rightarrow\) (2x . x) + x - 18 chia hết cho x - 3
\(\Rightarrow\) 3x + x - 18 chia hết cho x - 3
\(\Rightarrow\) 4x - 18 chia hết cho x - 3
\(\Rightarrow\) 4x - 12 - 6 chia hết cho x - 3
\(\Rightarrow\) 4(x - 3) - 6 chia hết cho x - 3
\(\Rightarrow\) (-6) chia hết cho x - 3
\(\Rightarrow\) x - 3 \(\in\) Ư(-6) = {-1; -2; -3; -6}
\(\Rightarrow\) x \(\in\) {2; 1; 0; -3}
b) 25 - y2 = 8(x - 2013)2
25 - y . y = 8(x - 2013)(x - 2013)
25 - 2y = 8 - 2(x - 2013)
25 - 2y = 8 - (2x - 2 . 2013)
25 - 2y = 8 - (2x - 4026)
25 - 2y = 8 - 2x + 4026
25 - 2y = (8 + 4026) - 2x
25 - 2y = 4034 - 2x
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = 4 + 3x - x2 ; b) y =
#Hỏi cộng đồng OLM
#Mẫu giáo

1. a) Tập xác định : D = R; y' = 3 - 2x => y' = 0 ⇔ x = .
Bảng biến thiên :
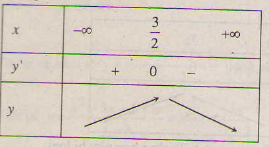
Hàm số đồng biến trên khoảng (-∞; ); nghịch biến trên khoảng (
; +∞ ).
b) Tập xác định D = R;
y'= x2 + 6x - 7 => y' = 0 ⇔ x = 1, x = -7.
Bảng biến thiên :
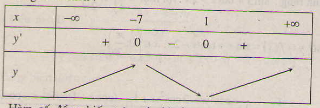
Hàm số đồng biến trên các khoảng (-∞ ; -7), (1 ; +∞) ; nghịch biến trên các khoảng (-7 ; 1).
c) Tập xác định : D = R.
y' = 4x3 - 4x = 4x(x2 - 1) => y' = 0 ⇔ x = -1, x = 0, x = 1.
Bảng biến thiên :
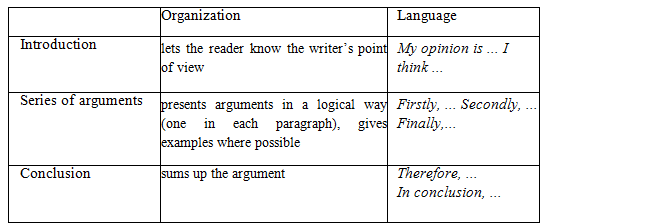
Hàm số đồng biến trên các khoảng (-1 ; 0), (1 ; +∞) ; nghịch biến trên các khoảng (-∞ ; -1), (0 ; 1).
d) Tập xác định : D = R. y' = -3x2 + 2x => y' = 0 ⇔ x = 0, x = .
Bảng biến thiên :
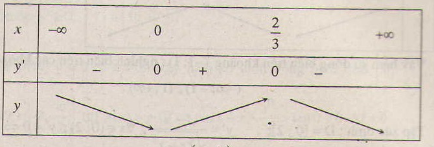
Hàm số đồng biến trên khoảng ( 0 ; ) ; nghịch biến trên các khoảng (-∞ ; 0),
( ; +∞).

\(A=\left(2x\right)^2-2.2x.5+5^2-4x.x+4x.6\)
\(=4x^2-20x+25-4x^2+24x=4x+25\)
\(B=\left(7x-3y\right)^2-\left(7x-3y\right)\left(7x+3y\right)\)
\(=\left(7x-3y\right)\left(7x-3y-7x-3y\right)\)
\(=\left(7x-3y\right)\left(-6y\right)=18y^2-42xy\)
\(C=\left(3-2x\right)^2+\left(3+2x\right)^2\)
\(=9-2.3.2x+4x^2+9+2.3.2x+4x^2\)
\(=18+8x^2\)
\(D=\left(x-y+z\right)^2+\left(z-y\right)^2+2\left(x-y+x\right)\left(y-z\right)\)
\(=\left(x-y+z+z-y\right)^2=x^2\)

a) A=2x^2-1/3y
thay x=2 và y=9 vào biểu thức:
Ta có :2.2^2-1/3.9
=2.4-3
= 6-3=3
Vậy tại x =2 và y=9 giá trị của biểu thức bằng 3
Bài 1. a) Bảng biến thiên :
Bảng biến thiên :
Hàm số đạt cực đại tại x = -3 , ycđ = y(-3) = 71
Hàm số đạt cực tiểu tại x = 2 ,
b) y’ = 4x3 + 4x = 4x(x2 + 1); y’ = 0 ⇔ x = 0.
Bảng biến thiên :
Hàm số đạt cực tiểu tại x = 0 , .
.
c) Tập xác định :
Bảng biến thiên :
Hàm số đạt cực đại tại x = -1 , ycđ = y(-1) = -2 ;
Hàm số đạt cực tiểu tại x = 1 , yct = y(1) = 2.
d) Tập xác định : D = R.
y’ = 3x2(1 – x)2 + x3 . 2(1 – x)(-1) = x2 (1 – x)[3(1 – x) - 2x] = x2 (x – 1)(5x – 3) .
y’ = 0 ⇔ x = 0, x = , x = 1.
, x = 1.
Bảng biến thiên :
Hàm số đạt cực đại tại x = , ycđ =
, ycđ =  =
=  ;
;
Hàm số đạt cực tiểu tại x = 1 , yct = y(1) = 0 .
e) Tập xác định : D = R.
Bảng biến thiên :
Hàm số đạt cực tiểu tại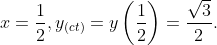
Bài 1. a) Bảng biến thiên :
Bảng biến thiên :
Hàm số đạt cực đại tại x = -3 , ycđ = y(-3) = 71
Hàm số đạt cực tiểu tại x = 2 ,
b) y’ = 4x3 + 4x = 4x(x2 + 1); y’ = 0 ⇔ x = 0.
Bảng biến thiên :
Hàm số đạt cực tiểu tại x = 0 , .
.
c) Tập xác định :
Bảng biến thiên :
Hàm số đạt cực đại tại x = -1 , ycđ = y(-1) = -2 ;
Hàm số đạt cực tiểu tại x = 1 , yct = y(1) = 2.
d) Tập xác định : D = R.
y’ = 3x2(1 – x)2 + x3 . 2(1 – x)(-1) = x2 (1 – x)[3(1 – x) - 2x] = x2 (x – 1)(5x – 3) .
y’ = 0 ⇔ x = 0, x = , x = 1.
, x = 1.
Bảng biến thiên :
Hàm số đạt cực đại tại x = , ycđ =
, ycđ =  =
=  ;
;
Hàm số đạt cực tiểu tại x = 1 , yct = y(1) = 0 .
e) Tập xác định : D = R.
Bảng biến thiên :
Hàm số đạt cực tiểu tại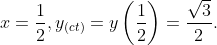
Xem thêm tại: http://loigiaihay.com/bai-1-trang-18-sach-sgk-giai-tich-12-c47a2683.html#ixzz44ZBz8Jsr