BU
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
S
subjects
CTVHS
22 tháng 8
bài 14:
\(a.\left(x-1\right)\cdot100=0\)
\(x-1=0\Rightarrow x=1\)
\(b.200-11x=24\)
\(11x=200-24\)
\(11x=176\)
\(x=\frac{176}{11}=16\)
\(c.165:\left(2x+1\right)=15\) (đkxđ: x khác \(-\frac12)\)
\(2x+1=\frac{165}{15}=11\)
\(2x=11-1=10\)
\(x=\frac{10}{2}=5\)
\(d.375:\left(45-4x\right)=15\) (đkxđ: \(x\ne\frac{45}{4})\)
\(45-4x=\frac{375}{15}=25\)
\(4x=45-25=20\)
\(x=20:4=5\)
bài 15:
giá tiền 125 chiếc điện thoại là:
125 x 2350000=293750000 (đồng)
giá tiền 250 chiếc máy tính bảng là:
250 x 4950000 = 1237500000 (đồng)
tổng số tiền mà cửa hàng phải trả cho số điện thoại và máy tính trên là:
293750000 + 1237500000 = 1531250000 (đồng)
đáp số: 1531250000 đồng
bài 16: từ năm 2022 đến năm 2025 có năm 2024 là năm nhuận
số ngày từ năm 2022 đến năm 2025 là:
365 x 4 + 1 = 1461 (ngày)
1461 : 7 = 208 dư 5
3 + 5 = 8 (chủ nhật)
vậy vào 9/3/2025 , sẽ rơi vào ngày chủ nhật trong tuần
16 tháng 8
Ta có: \(\frac{A}{10^{10}}=\frac{10^{20}-6}{10^{20}-6\cdot10^{10}}=\frac{10^{20}-6\cdot10^{10}+6\left(10^{10}-1\right)}{10^{20}-6\cdot10^{10}}=1+\frac{6\left(10^{10}-1\right)}{10^{20}-6\cdot10^{10}}\)
\(\frac{B}{10^{10}}=\frac{10^{21}-6}{10^{21}-6\cdot10^{10}}=\frac{10^{21}-6\cdot10^{10}+6\left(10^{10}-1\right)}{10^{21}-6\cdot10^{10}}=1+\frac{6\left(10^{10}-1\right)}{10^{21}-6\cdot10^{10}}\)
Ta có: \(10^{20}<10^{21}\)
=>\(10^{20}-6\cdot10^{10}<10^{21}-6\cdot10^{10}\)
=>\(\frac{6\left(10^{10}-1\right)}{10^{20}-6\cdot10^{10}}>\frac{6\left(10^{10}-1\right)}{10^{21}-6\cdot10^{10}}\)
=>\(\frac{6\left(10^{10}-1\right)}{10^{20}-6\cdot10^{10}}+1>\frac{6\left(10^{10}-1\right)}{10^{21}-6\cdot10^{10}}+1\)
=>\(\frac{A}{10^{10}}>\frac{B}{10^{10}}\)
=>A>B
16 tháng 8
Ta có: \(10A=\frac{10^{21}-60}{10^{21}-6}=\frac{10^{21}-6-54}{10^{21}-6}=1-\frac{54}{10^{21}-6}\)
\(10B=\frac{10^{22}-60}{10^{22}-6}=\frac{10^{22}-6-54}{10^{22}-6}=1-\frac{54}{10^{22}-6}\)
Ta có: \(10^{21}-6<10^{22}-6\)
=>\(\frac{54}{10^{21}-6}>\frac{54}{10^{22}-6}\)
=>\(-\frac{54}{10^{21}-6}<-\frac{54}{10^{22}-6}\)
=>\(-\frac{54}{10^{21}-6}+1<-\frac{54}{10^{22}-6}+1\)
=>10A<10B
=>A<B
23 tháng 8
bài 3:
a: \(C=5+5^2+5^3+\cdots+5^{20}\)
\(=5\left(1+5+5^2+\cdots+5^{19}\right)\) ⋮5
b: \(C=5+5^2+5^3+\cdots+5^{20}\)
\(=\left(5+5^2\right)+\left(5^3+5^4\right)+\cdots+\left(5^{19}+5^{20}\right)\)
\(=5\left(1+5\right)+5^3\left(1+5\right)+\cdots+5^{19}\left(1+5\right)\)
\(=6\left(5+5^3+\cdots+5^{19}\right)\) ⋮6
c: \(C=5+5^2+5^3+\cdots+5^{20}\)
\(=\left(5+5^2+5^3+5^4\right)+\left(5^5+5^6+5^7+5^8\right)+\cdots+\left(5^{17}+5^{18}+5^{19}+5^{20}\right)\)
\(=5\left(1+5+5^2+5^3\right)+5^5\left(1+5+5^2+5^3\right)+\cdots+5^{17}\left(1+5+5^2+5^3\right)\)
\(=\left(1+5+5^2+5^3\right)\left(5+5^5+\cdots+5^{17}\right)=156\cdot\left(5+5^5+\cdots+5^{17}\right)\)
\(=13\cdot12\cdot\left(5+5^5+\cdots+5^{17}\right)\) ⋮13
Bài 2:
a: \(B=3+3^2+3^3+\cdots+3^{120}\)
\(=3\left(1+3+3^2+3^3+\cdots+3^{119}\right)\) ⋮3
b: \(B=3+3^2+3^3+\cdots+3^{120}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+\cdots+\left(3^{119}+3^{120}\right)\)
\(=3\left(1+3\right)+3^3\left(1+3\right)+\cdots+3^{119}\left(1+3\right)\)
\(=4\left(3+3^3+\cdots+3^{119}\right)\) ⋮4
c: \(B=3+3^2+3^3+\cdots+3^{120}\)
\(=\left(3+3^2+3^3\right)+\left(3^4+3^5+3^6\right)+\cdots+\left(3^{118}+3^{119}+3^{120}\right)\)
\(=3\left(1+3+3^2\right)+3^4\left(1+3+3^2\right)+\cdots+3^{118}\left(1+3+3^2\right)\)
\(=13\left(3+3^4+\cdots+3^{118}\right)\) ⋮13
Bài 1:
a: \(A=2+2^2+2^3+\ldots+2^{20}\)
\(=2\left(1+2+2^2+\cdots+2^{19}\right)\) ⋮2
b: \(A=2+2^2+2^3+\ldots+2^{20}\)
\(=\left(2+2^2\right)+\left(2^3+2^4\right)+\cdots+\left(2^{19}+2^{20}\right)\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+\cdots+2^{19}\left(1+2\right)\)
\(=3\left(2+2^3+\cdots+2^{19}\right)\) ⋮3
c: \(A=2+2^2+2^3+\ldots+2^{20}\)
\(=\left(2+2^2+2^3+2^4\right)+\left(2^5+2^6+2^7+2^8\right)+\cdots+\left(2^{17}+2^{18}+2^{19}+2^{20}\right)\)
\(=2\left(1+2+2^2+2^3\right)+2^5\left(1+2+2^2+2^3\right)+\cdots+2^{17}\left(1+2+2^2+2^3\right)\)
\(=15\left(2+2^5+\ldots+2^{17}\right)=5\cdot3\cdot\left(2+2^5+\cdots+2^{17}\right)\) ⋮5
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
23 tháng 8
Bài 1:
a; A = 2 + \(2^2\) + 2\(^3\) + ... + 2\(^{20}\)
A = 2 x (1+ 2+ 2\(^2\) + ... + 2\(^{19}\))
A ⋮ 2(đpcm)
b; A = 2 + \(2^2\) + 2\(^3\) + ... + 2\(^{20}\)
Xét dãy số: 1; 2;...; 20 đây là dãy số cách đều với khoảng cách là:
2 - 1 = 1
Số số hạng của dãy số trên là:
(20 - 1) : 1+ 1 = 20(số)
Vì 20 : 2 = 10
Vậy nhóm hai số hạng liên tiếp của A vào nhau khi đó ta có:
A = (2+ 2\(^2\)) + (2\(^3\) + 2\(^4\)) + ... + (2\(^{19}+\) 2\(^{20}\))
A = 2.(1 + 2) + 2\(^3\).(1+ 2) + ... + 2\(^{19}\) .(1 + 2)
A = 2.3 + 2\(^3\).3 + ... + 2\(^{19}\).3
A = 3.(2+ 2\(^3\) + ... + 2\(^{19}\))
A ⋮ 3 (đpcm)
c; A = 2 + \(2^2\) + 2\(^3\) + ... + 2\(^{20}\)
Xét dãy số: 1; 2; 3;...; 20
Dãy số trên có 20 số hạng:
Vì 20 : 4 = 5
Vậy nhóm 4 hạng tử của A thành một nhóm khi đó:
A = (2+ 2\(^2\) + 2\(^3\) + 2\(^4\)) + ... + (2\(^{17}+2^{18}+2^{19}+2^{20}\))
A = 2.(1 + 2 + 2\(^2\) + 2\(^3\)) + ... + 2\(^{17}\).(1 + 2 + 2\(^2\) + 2\(^3\))
A = (1+ 2 +2\(^2\) + 2\(^3\)).(2+ ...+ 2\(^{17}\))
A = (1 + 2 + 4 + 8).(2+ ...+ 2\(^{17}\))
A = (3+ 4 + 8).(2+ ...+ 2\(^{17}\))
A = (7 + 8)(2+ ...+ 2\(^{17}\))
A = 15.(2+ ...+ 2\(^{17}\))
A ⋮ 5(đpcm)
23 tháng 8
Bài 8:
a: \(5^3=125;3^5=243\)
mà 125<243
nên \(5^3<3^5\)
b: \(7\cdot2^{13}<8\cdot2^{13}=2^3\cdot2^{13}=2^{16}\)
c: \(27^5=\left(3^3\right)^5=3^{3\cdot5}=3^{15}\)
\(243^3=\left(3^5\right)^3=3^{5\cdot3}=3^{15}\)
Do đó: \(27^5=243^5\)
d: \(625^5=\left(5^4\right)^5=5^{4\cdot5}=5^{20}\)
\(125^7=\left(5^3\right)^7=5^{3\cdot7}=5^{21}\)
mà 20<21
nên \(625^5<125^7\)
Bài 9:
a: \(3^{x}\cdot5=135\)
=>\(3^{x}=\frac{135}{5}=27=3^3\)
=>x=3(nhận)
b: \(\left(x-3\right)^3=\left(x-3\right)^2\)
=>\(\left(x-3\right)^3-\left(x-3\right)^2=0\)
=>\(\left(x-3\right)^2\cdot\left\lbrack\left(x-3\right)-1\right\rbrack=0\)
=>\(\left(x-3\right)^2\cdot\left(x-4\right)=0\)
=>\(\left[\begin{array}{l}x-3=0\\ x-4=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=3\left(nhận\right)\\ x=4\left(nhận\right)\end{array}\right.\)
c: \(\left(2x-1\right)^4=81\)
=>\(\left[\begin{array}{l}2x-1=3\\ 2x-1=-3\end{array}\right.\Rightarrow\left[\begin{array}{l}2x=4\\ 2x=-2\end{array}\right.\Rightarrow\left[\begin{array}{l}x=2\left(nhận\right)\\ x=-1\left(loại\right)\end{array}\right.\)
d: \(\left(5x+1\right)^2=3^2\cdot5+76\)
=>\(\left(5x+1\right)^2=9\cdot5+76=45+76=121\)
=>\(\left[\begin{array}{l}5x+1=11\\ 5x+1=-11\end{array}\right.\Rightarrow\left[\begin{array}{l}5x=10\\ 5x=-12\end{array}\right.\Rightarrow\left[\begin{array}{l}x=2\left(nhận\right)\\ x=-\frac{12}{5}\left(loại\right)\end{array}\right.\)
e: \(5+2^{x-3}=29-\left\lbrack4^2-\left(3^2-1\right)\right\rbrack\)
=>\(2^{x-3}+5=29-\left\lbrack16-9+1\right\rbrack\)
=>\(2^{x-3}+5=29-8=21\)
=>\(2^{x-3}=16=2^4\)
=>x-3=4
=>x=4+3=7(nhận)
f: \(3+2^{x-1}=24-\left\lbrack4^2-\left(2^2-1\right)\right\rbrack\)
=>\(2^{x-1}+3=24-\left\lbrack16-4+1\right\rbrack=24-13=11\)
=>\(2^{x-1}=11-3=8=2^3\)
=>x-1=3
=>x=4(nhận)
Bài 6:
a: \(5\cdot5\cdot5\cdot5\cdot5\cdot5=5^6\)
b: \(27\cdot14\cdot7\cdot2=27\cdot14\cdot14=3^3\cdot14^2\)
c: \(x\cdot x\cdot x\cdot y=x^3\cdot y\)
d: \(5^3\cdot5^4=5^{3+4}=5^7\)
e: \(7^8:7^2=7^{8-2}=7^6\)
f: \(42^7:6^7\cdot49=7^7\cdot49=7^7\cdot7^2=7^{7+2}=7^9\)
CT
6
NV
11 tháng 8 2023
Quy luật: Hiệu của số lớn hơn trừ cho số nhỏ hơn trong mổi ô chính là kết quả của ô màu vàng đối diện
17-13=4
15-6=9
14-8=6
19-12=7
23-15=8
27-25=2
23-18=5
Suy ra: 12-x=3
=> x=12-3=9
Đáp án C
11 tháng 8 2023
Giải thích: Mỗi số trong hình tam giác màu vàng bằng số lớn hơn của hình bình hành đối diện trừ đi số bé hơn ở hình bình hành đối diện.
=> ? - 12 = 3 hoặc 12 - ? = 3
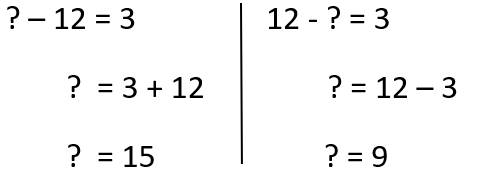
=> Đáp án là 15 hoặc 9
Đáp án: c
Bổ sung: Đáp án cũng có thể là 15
CT
18
P
Phong
CTVHS
17 tháng 8 2023
Ta có các quy luật sau:
\(\left(1+3\right)-2=2\)
\(\left(2+2\right)-3=1\)
\(\left(5+5\right)-6=4\)
Vậy dòng cuối là:
\(\left(5+9\right)-5=9\)
Số điền vào là 9
(Quy luật: lấy 2 số phía dưới cộng với nhau rồi trừ cho số phía trên sẽ ra được số ở giữa)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 8
a; \(x-33=28\)
\(x=28+33\)
\(x=61\)
Vậy \(x=61\)
b; \(x+55\) = 122
\(x=122-55\)
\(x=\) 67
Vậy \(x=67\)
c; \(x\times34\) = 37
\(x\) = 37 : 34
\(x=\frac{37}{34}\)
Vậy \(x=\frac{37}{34}\)
d; \(x:23\) = 7
\(x=7\times23\)
\(x=161\)
Vậy \(x=161\)
e; \(x^2=81\)
\(x=9^2\)
\(\left[\begin{array}{l}x=-9\\ x=9\end{array}\right.\)
Vậy \(x\in\) {-9; 9}
f; (\(x-3)^3\) = 27
(\(x-3)^3=3^3\)
\(x-3=3\)
\(x=3+3\)
\(x=6\)
Vậy \(x=6\)
TP
22 tháng 8
a; \(x - 33 = 28\)
\(x = 28 + 33\)
\(x = 61\)
Vậy \(x = 61\)
b; \(x + 55\) = 122
\(x = 122 - 55\)
\(x =\) 67
Vậy \(x = 67\)
c; \(x \times 34\) = 37
\(x\) = 37 : 34
\(x = \frac{37}{34}\)
Vậy \(x = \frac{37}{34}\)
d; \(x : 23\) = 7
\(x = 7 \times 23\)
\(x = 161\)
Vậy \(x = 161\)
e; \(x^{2} = 81\)
\(x = 9^{2}\)
\(\left[\right. x = - 9 \\ x = 9\)
Vậy \(x \in\) {-9; 9}
f; (\(x - 3 \left.\right)^{3}\) = 27
(\(x - 3 \left.\right)^{3} = 3^{3}\)
\(x - 3 = 3\)
\(x = 3 + 3\)
\(x = 6\)
Vậy \(x = 6\)
CC
2
27 tháng 8
Câu 8:
a:Sửa đề: \(4+4^2+\cdots+4^{2025}\)
Ta có: \(4+4^2+\cdots+4^{2025}\)
\(=\left(4+4^2+4^3\right)+\left(4^4+4^5+4^6\right)+\cdots+\left(4^{2023}+4^{2024}+4^{2025}\right)\)
\(=4\left(1+4+4^2\right)+4^4\left(1+4+4^2\right)+\cdots+4^{2023}\left(1+4+4^2\right)\)
\(=21\left(4+4^4+\cdots+4^{2023}\right)\) ⋮21
b: \(5+5^2+5^3+5^4+\cdots+5^{2024}\)
\(=\left(5+5^2\right)+\left(5^3+5^4\right)+\cdots+\left(5^{2023}+5^{2024}\right)\)
\(=\left(5+5^2\right)+5^2\left(5+5^2\right)+\cdots+5^{2022}\left(5+5^2\right)\)
\(=30\left(1+5^2+\cdots+5^{2022}\right)\) ⋮30
Câu 7:
a: \(A=2+2^2+2^3+\cdots+2^{99}\)
=>\(2A=2^2+2^3+\cdots+2^{100}\)
=>\(2A-A=2^2+2^3+\cdots+2^{100}-2-2^2-\cdots-2^{99}\)
=>\(A=2^{100}-2\)
b: \(B=1-7+7^2-7^3+\cdots+7^{48}-7^{49}\)
=>\(7B=7-7^2+7^3-7^4+\cdots+7^{49}-7^{50}\)
=>\(7B+B=7-7^2+7^3-7^4+\cdots+7^{49}-7^{50}+1-7+7^2-7^3+\cdots+7^{48}-7^{49}\)
=>\(8B=-7^{50}+1\)
=>\(B=\frac{-7^{50}+1}{8}\)
Câu 4:
a: \(x^3=125\)
=>\(x^3=5^3\)
=>x=5
b: \(11^{x+1}=121\)
=>\(11^{x+1}=11^2\)
=>x+1=2
=>x=2-1=1
c: \(\left(x-5\right)^3=27\)
=>\(\left(x-5\right)^3=3^3\)
=>x-5=3
=>x=3+5=8
d: \(4^5:4^{x}=16\)
=>\(4^{x}=4^5:16=4^5:4^2=4^3\)
=>x=3
e: \(5^{x-1}\cdot8=1000\)
=>\(5^{x-1}=1000:8=125=5^3\)
=>x-1=3
=>x=3+1=4
f: \(2^{x}+2^{x+3}=72\)
=>\(2^{x}+2^{x}\cdot8=72\)
=>\(2^{x}\cdot9=72\)
=>\(2^{x}=\frac{72}{9}=8=2^3\)
=>x=3
g: \(\left(3x+1\right)^3=343\)
=>\(\left(3x+1\right)^3=7^3\)
=>3x+1=7
=>3x=6
=>x=2
h: \(3^{x}+3^{x+2}=270\)
=>\(3^{x}+3^{x}\cdot9=270\)
=>\(10\cdot3^{x}=270\)
=>\(3^{x}=\frac{270}{10}=27=3^3\)
=>x=3
i: \(25^{2x+4}=125^{x+3}\)
=>\(\left(5^2\right)^{2x+4}=\left(5^3\right)^{x+3}\)
=>\(5^{4x+8}=5^{3x+9}\)
=>4x+8=3x+9
=>x=1
Câu 6:
1 giờ=3600 giây
Số tế bào hồng cầu được tạo ra sau mỗi giờ là:
\(25\cdot10^5\cdot3600=25\cdot36\cdot10^7=900\cdot10^7=9\cdot10^9\) =9 tỉ (tế bào)
S
subjects
CTVHS
28 tháng 8
câu 5:
a. \(16^{16}=\left(2^4\right)^{16}=2^{64}\)
\(64^{11}=\left(2^6\right)^{11}=2^{66}\)
vì \(2^{66}>2^{64}\) nên \(64^{11}>16^{16}\)
b. \(625^5=\left(5^4\right)^5=5^{20}\)
\(125^7=\left(5^3\right)^7=5^{21}\)
\(5^{20}<5^{21}\Rightarrow625^5<125^7\)
c. \(3^{36}=\left(3^3\right)^{12}=27^{12}\)
\(5^{24}=\left(5^2\right)^{12}=25^{12}\)
\(27^{12}>25^{12}\Rightarrow3^{36}>5^{24}\)
3.
\(C=5+5^2+...+5^6\\ C=5\left(1+5\right)+5^3\left(1+5\right)+5^5\left(1+5\right)\\ C=5\cdot6+5^3\cdot6+5^5\cdot6\\ C=6\left(5+5^3+5^5\right)\\ =>C⋮6\)
\(4.D=3+3^2+...+3^6\\D=3\left(1+3\right)+3^3\left(1+3\right)+3^5\left(1+3\right)\\ D=3\cdot4+3^3\cdot4+3^5\cdot5\\ C=4\left(3+3^3+3^5\right)\\ =>D⋮4\\ 5.E=4+4^2+...+4^6\\ E=4\left(1+4\right)+4^3\left(1+4\right)+4^5\left(1+4\right)\\ E=4\cdot5+4^3\cdot5+4^5\cdot5\\ E=5\left(4+4^3+4^5\right)=>E⋮5 \)