Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

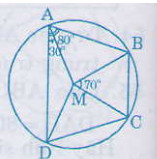
Ta có: =
-
= 80o – 30o = 50o (1)
- ∆MBC là tam giác cân (MB= MC) nên =
= 55o (2)
- ∆MAB là tam giác cân (MA=MB) nên = 50o (theo (1))
Vậy = 180o – 2. 50o = 80o
=
sđcung BCD (số đo góc nội tiếp bằng nửa số đo của cung bị chắn)
=> sđ cung BCD = 2 = 2. 80o = 160o
Mà sđ cung BC = = 70o (số đo ở tâm bằng số đo cung bị chắn)
Vậy cung DC = 160o – 70o = 90o (vì C nằm trên cung nhỏ cung BD)
Suy ra = 90o (4)
∆MAD là tam giác cân (MA= MD)
Suy ra = 180o – 2.30o = 120o (5)
∆MCD là tam giác vuông cân (MC= MD) và = 90o
Suy ra =
= 45o (6)
= 100o theo (2) và (6) và vì CM là tia nằm giữa hai tia CB, CD

Ta có: =
-
= 80o – 30o = 50o (1)
- ∆MBC là tam giác cân (MB= MC) nên =
= 55o (2)
- ∆MAB là tam giác cân (MA=MB) nên = 50o (theo (1))
Vậy = 180o – 2. 50o = 80o
=
sđcung BCD (số đo góc nội tiếp bằng nửa số đo của cung bị chắn)
=> sđ cung BCD = 2 = 2. 80o = 160o
Mà sđ cung BC = = 70o (số đo ở tâm bằng số đo cung bị chắn)
Vậy cung DC = 160o – 70o = 90o (vì C nằm trên cung nhỏ cung BD)
Suy ra = 90o (4)
∆MAD là tam giác cân (MA= MD)
Suy ra = 180o – 2.30o = 120o (5)
∆MCD là tam giác vuông cân (MC= MD) và = 90o
Suy ra =
= 45o (6)
= 100o theo (2) và (6) và vì CM là tia nằm giữa hai tia CB, CD

Hình bạn tự vẽ nha. a) CM tứ giác MIOD là tứ giác nt, suy ra 4 điểm M,I,O,D cùng nằm trên đường tròn đk OM. Cm tiếp cho tứ giác MCOD là TGNT, suy ra 4 điểm M,C,O,D cùng nằm trên đtròn đk OM, vì thế 5 điểm M,I,O,C,D cùng nằm trên 1 đtròn, suy ra MCID nt c) Vì MCID nt suy ra \(\widehat{MIC}\)=\(\widehat{MDC}\), \(\widehat{MID}=\widehat{MCD}\). mà \(\widehat{MCD}=\widehat{MDC}\) nên 2 góc còn lại bằng nhau, ta đc ĐPCM. Còn câu b à d bn đợi xíu nha, nếu đc mk đăng lên cho nha

M A B C K H O D
Mk chỉ kịp làm câu a thôi sorry nha!
Dễ dàng chứng minh được tam giác MAB và tam giác MCD đều vuông góc tại M ( CM theo bài 7 chương I sách GK toán 9)
\(\Rightarrow Sin^2\angle MCD=Cos^2\angle MDC \)
và
\(\Rightarrow Sin^2\angle MAB=Cos^2\angle MBA \)
thay vào ta có: \(sin^2\angle MBA+ sin^2\angle MAB + sin^2\angle MCD+sin^2\angle MDC \)
\(=sin^2\angle MBA+ cos^2\angle MBA + cos^2\angle MDC+sin^2\angle MDC\)
\(=(sin^2\angle MBA+ cos^2\angle MBA) + (cos^2\angle MDC+sin^2\angle MDC)\)
\(= 1+1=2\)
Hỏi hay là trả lời vậy?