Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: A(1;2); B(2;1)
=>\(\overrightarrow{AB}=\left(1;-1\right)\)
=>VTPT là (1;1)
Phương trình đường thẳng AB là:
1(x-1)+2(y-1)=0
=>x-1+2y-2=0
=>x+2y-3=0
b:
M(1;3); Δ: 3x+4y+10=0
Khoảng cách từ M đến Δ là:
\(d\left(M;\text{Δ}\right)=\dfrac{\left|1\cdot3+3\cdot4+10\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|3+12+10\right|}{5}=5\)

Đáp án A
Ta có: ![]()
AM → (3; 2; 4)
Mặt phẳng (P) có vecto pháp tuyến là n p → (1; 1; 1)
Gọi H là hình chiếu vuông góc của A trên d. Ta có: d(A; d) = AH ≤ AM = 29
Dấu bằng xảy ra khi và chỉ khi H trùng M, nghĩa là d vuông góc với AM.
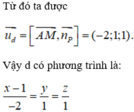

a/ CD qua E và vuông góc BC nên pt có dạng:
\(1\left(x-6\right)-1\left(y-0\right)=0\Leftrightarrow x-y-6=0\)
Ta có: \(AB=d\left(A;BC\right)=\frac{\left|3+5-2\right|}{\sqrt{1^2+1^2}}=3\sqrt{2}\)
\(AD=d\left(A;CD\right)=\frac{\left|3-5-6\right|}{\sqrt{1^2+\left(-1\right)^2}}=4\sqrt{2}\)
\(\Rightarrow S_{ABCD}=AB.AD=24\)
b/ Do M thuộc d nên tọa độ có dạng: \(M\left(1+t;2-3t\right)\)
Áp dụng công thức khoảng cách:
\(d\left(M;\Delta\right)=4\Leftrightarrow\frac{\left|3\left(1+t\right)+4\left(2-3t\right)+5\right|}{\sqrt{3^2+4^2}}=4\)
\(\Leftrightarrow\left|16-9t\right|=20\Rightarrow\left[{}\begin{matrix}16-9t=20\\16-9t=-20\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}t=-\frac{4}{9}\\t=4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}M\left(\frac{5}{9};\frac{10}{3}\right)\\M\left(5;-10\right)\end{matrix}\right.\)

\(1/\)
\(M\left(3;5\right);d:x+y+1=0\)
\(\)Gọi khoảng cách từ M đến d là \(l\)
\(l\left(M;d\right)=\dfrac{\left|x_M+y_M+1\right|}{\sqrt{1^2+1^2}}=\dfrac{\left|3+5+1\right|}{\sqrt{1^2+1^2}}=\dfrac{9\sqrt{2}}{2}\)
\(M\left(2;3\right);d:\left\{{}\begin{matrix}x-2t\\y=2+3t\end{matrix}\right.\)
d qua \(M\left(2;3\right)\) có \(VTCP\overrightarrow{u}=\left(-2;3\right)\Rightarrow VTPT\overrightarrow{n}=\left(3;2\right)\)
\(PTTQ\) của \(\Delta:3\left(x-2\right)+2\left(y-3\right)=0\)
\(\Rightarrow3x-6+2y-6=0\)
\(\Rightarrow3x+2y-12=0\)
Gọi khoảng cách từ M đến d là \(l\)
\(l\left(M;d\right)=\dfrac{\left|3.x_M+2.y_M-12\right|}{\sqrt{3^2+2^2}}=\dfrac{\left|3.2+2.3-12\right|}{\sqrt{3^2+2^2}}=0\)


1.
\(d\left(A;d\right)=\frac{\left|3.1-4.3+4\right|}{\sqrt{3^2+\left(-4\right)^2}}=\frac{5}{5}=1\)
2. Đường thẳng d qua \(Q\left(2;5\right)\) và nhận \(\left(1;-3\right)\) là 1 vtcp nên nhận \(\left(3;1\right)\) là 1 vtpt
Pt tổng quát: \(3\left(x-2\right)+1\left(y-5\right)=0\Leftrightarrow3x+y-11=0\)
\(\Rightarrow d\left(P;d\right)=\frac{\left|3.3+12.1-11\right|}{\sqrt{3^2+1^2}}=\frac{10}{\sqrt{10}}=\sqrt{10}\)