K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
0
MC
4 tháng 7 2018
\(a)3^5.3.3^{10}:3^{15}=3^{5+1+10-15}=3\)
\(b)4^8.2^5.8^3=\left(2^2\right)^8.2^5.\left(2^3\right)^3=2^{16}.2^5.2^9=2^{16+5+9}=2^{30}\)
\(c)16^2:4^3=\left(4^2\right)^2:4^3=4^4:4^3=4\)
KK
4 tháng 7 2018
a,x2- 22 = 32
⇔ x2=32+22
⇔ x2=36
⇔ x= \(\pm6\)
vậy x=\(\pm6\)
b,x3+ 5 =4
⇔ x3=4-5
⇔ x3=-1
⇔ x=-1
vậy x=-1
c, x3- 4.x= 0
⇔ x(x2-4)=0
⇔ x(x-2)(x+2)=0
⇔ \(\left[{}\begin{matrix}x=0\\x-2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
vậy .....
CM
9 tháng 7 2017
Đáp án B
- Ta có (C1) với tâm I(5; -12) và R= 15.
(C2) có tâm J( 1;2) và R’ =5 .
Gọi d là tiếp tuyến chung có phương trình: ax+ by+ c= 0 ().
- Khi đó ta có :
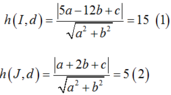
- Từ (1) và (2) suy ra :
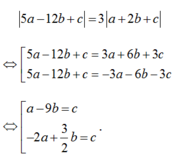
Thay vào (1):
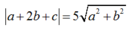
Ta có hai trường hợp :
- Trường hợp : c = a-9b thay vào (1):
(2a- 7b)2= 25 (a2+ b2)
hay 21a2+ 28ab -24b2= 0
Suy ra :
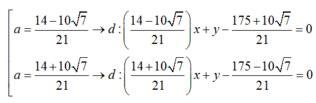
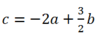
(1) => ( 7b- 2a)2=100(a2+b2) hay 96a2+ 28ab + 51b2= 0
Vô nghiệm.
Vậy 2 đường tròn đã cho có 2 tiếp tuyến chung.
26 tháng 2 2020
a) 11+(15-x)=1
⇔15-x=-10
hay x=25
Vậy: x=25
b) 2x-35=15
⇔2x=50
hay x=25
Vậy: x=25
c) 2|x+5|=12
⇔|x+5|=6
\(\Leftrightarrow\left[{}\begin{matrix}x+5=6\\x+5=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-11\end{matrix}\right.\)
Vậy: x∈{1;-11}
8 tháng 4 2020
A/ \( 11+(15-x)=1\)\(\Leftrightarrow11+15-x=1\Leftrightarrow x=11+15-1=25\)
KL: ...........
B/ \(2x-35=15\Leftrightarrow2x=15+35=50\Leftrightarrow x=25\)
KL: ............
C/ \(2\left|x+5\right|=12\Leftrightarrow\left|x+5\right|=6\Leftrightarrow\left[{}\begin{matrix}x+5=6\\x+5=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-11\end{matrix}\right.\)
KL: .............
12 tháng 5 2022
\(\dfrac{3}{4\left(x-5\right)}-\dfrac{15}{2\left(x-5\right)\left(x+5\right)}=\dfrac{-7}{6\left(x+5\right)}\)
\(\Leftrightarrow9\left(x+5\right)-90=-14\left(x-5\right)\)
=>9x+45-90=-14x+70
=>23x=70-45+90=115
hay x=5(loại)
N
0
NT
1
9 tháng 6 2022
a: \(3x^2-5x+7\)
\(=3\left(x^2-\dfrac{5}{3}x+\dfrac{7}{3}\right)\)
\(=3\left(x^2-2\cdot x\cdot\dfrac{5}{6}+\dfrac{25}{36}+\dfrac{59}{36}\right)\)
\(=3\left(x-\dfrac{5}{6}\right)^2+\dfrac{59}{12}\ge\dfrac{59}{12}\)
Dấu '=' xảy ra khi x=5/6
c: \(\left(x-3\right)^2+\left(x-2\right)^2\)
\(=x^2-6x+9+x^2-4x+4\)
\(=2x^2-10x+13\)
\(=2\left(x^2-5x+\dfrac{13}{2}\right)\)
\(=2\left(x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}+\dfrac{1}{4}\right)\)
\(=2\left(x-\dfrac{5}{2}\right)^2+\dfrac{1}{2}\ge\dfrac{1}{2}\)
Dấu '=' xảy ra khi x=5/2
d: \(\left(x-1\right)\left(x+3\right)+11\)
\(=x^2+2x-3+11\)
\(=x^2+2x+8=\left(x+1\right)^2+7\ge7\)
Dấu '=' xảy ra khi x=-1
(15+x).5+x=225
<=>75+5x+x=225
<=>6x=150
<=>x=15
Vậy tập nghiệm S={15}