Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi đường thẳng đi qua M(3;4) và song song với \(\left(d\right):y=2x+6\)là \(\left(d'\right):y=a'x+b'\)
Vì \(\left(d'\right)//\left(d\right)\Rightarrow a'=2\)
Vậy phương trình đường thẳng (d') có dạng \(\left(d'\right):y=2x+b'\)
Mặt khác (d') đi qua M(3;4) nên điểm M(3;4) thuộc \(\left(d'\right):y=2x+b'\)
Thay \(x=3;y=4\)vào hàm số \(y=2x+b'\)ta có:
\(4=2.3+b'\Leftrightarrow b'=-2\)
Vậy phương trình đường thẳng đi qua M(3;4) và song song với \(\left(d\right):y=2x+6\)là \(\left(d'\right):y=2x-2\)
b) Gọi OH là khoảng cách từ O đến (d). Gọi giao điểm của (d):y = 2x + 6 với hai trục Ox, Oy lần lượt là A(xA;0), B(0;yB).
Thay x = xA; y = 0 vào hàm số y = 2x + 6, ta có: \(0=2x_A+6\Leftrightarrow x_A=-3\)
Thay x = 0; y = yB vào hàm số y = 2x + 6, ta có: \(y_B=2.0+6=6\)
Vì \(OA=\left|x_A\right|;OB=\left|y_B\right|\)\(\Rightarrow OA=\left|-3\right|=3;OB=\left|6\right|=6\)
\(\Delta OAB\)vuông tại O, đường cao OH \(\Rightarrow\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}\left(htl\right)\)
Rồi bạn thay OA, OB vào và dễ dàng tính được OH

a:Thay x=-2 và y=0 vào (d), ta được:
-2(m-1)+4=0
=>-2(m-1)=-4
=>m-1=2
=>m=3
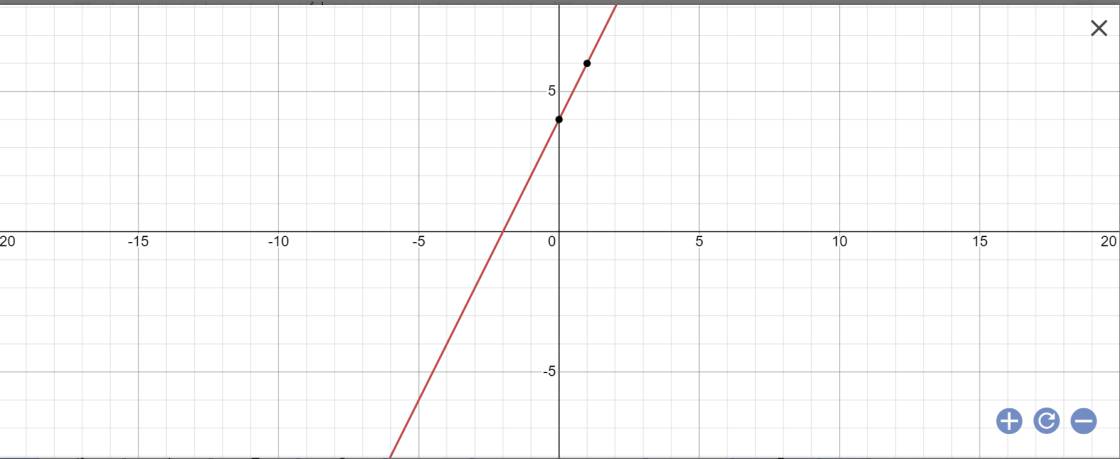
b: (d): y=2x+4

\(\Leftrightarrow mx+2x+my-y-1=0\)
\(\Leftrightarrow m\left(x+y\right)+2x-y-1=0\)
\(\Rightarrow d\) luôn đi qua điểm cố định A có tọa độ là nghiệm của hệ:
\(\left\{{}\begin{matrix}x+y=0\\2x-y-1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\frac{1}{3}\\y=-\frac{1}{3}\end{matrix}\right.\) \(\Rightarrow A\left(\frac{1}{3};-\frac{1}{3}\right)\)
Gọi H là hình chiếu vuông góc của O lên d \(\Rightarrow OAH\) vuông tại H
\(\Rightarrow OH\le OA\Rightarrow OH_{max}=OA\) khi \(H\) trùng A \(\Rightarrow d\perp OA\)
Phương trình OA có dạng: \(y=-x\)
\(\Rightarrow\) d có hệ số góc bằng 1
\(\left(m+2\right)x+\left(m-1\right)y-1=0\Rightarrow y=\frac{m+2}{1-m}x-\frac{1}{1-m}\)
\(\Rightarrow\frac{m+2}{1-m}=1\Rightarrow m+2=1-m\Rightarrow m=-\frac{1}{2}\)

Gọi A và B lần lượt là giao điểm của d với Ox và Oy
\(\Rightarrow A\left(-2;0\right)\) và \(B\left(0;2\right)\) \(\Rightarrow\left\{{}\begin{matrix}OA=\left|x_A\right|=2\\OB=\left|y_B\right|=2\end{matrix}\right.\)
\(\Rightarrow\Delta OAB\) vuông cân tại O
Gọi H là hình chiếu vuông góc của O lên d \(\Rightarrow OH=d\left(O;d\right)\)
Mặt khác do OAB vuông cân \(\Rightarrow\) OH là đường cao đồng thời là trung tuyến
\(\Rightarrow OH=\dfrac{1}{2}BC=\dfrac{1}{2}\sqrt{OA^2+OB^2}=\sqrt{2}\)

PT giao Ox, Oy là:
\(y=0\Leftrightarrow x=\dfrac{2}{2m+1}\Leftrightarrow A\left(\dfrac{2}{2m+1};0\right)\Leftrightarrow OA=\dfrac{2}{\left|2m+1\right|}\\ x=0\Leftrightarrow y=-2\Leftrightarrow B\left(0;-2\right)\Leftrightarrow OB=2\)
\(a,\) Gọi H là chân đường cao từ O đến (d) \(\Leftrightarrow OH=\sqrt{2}\)
Ap dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{\left(2m+1\right)^2}{4}+\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{\left(2m+1\right)^2}{4}=\dfrac{1}{4}\Leftrightarrow4m^2+4m+1=1\\ \Leftrightarrow4m\left(m+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=-1\end{matrix}\right.\)
\(b,S_{AOB}=\dfrac{1}{2}OA\cdot OB=\dfrac{1}{2}\Leftrightarrow OB\cdot OA=1\\ \Leftrightarrow\dfrac{2}{\left|2m+1\right|}\cdot2=1\Leftrightarrow\left|2m+1\right|=4\\ \Leftrightarrow\left[{}\begin{matrix}2m+1=4\\2m+1=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3}{2}\\m=-\dfrac{5}{2}\end{matrix}\right.\)
Lời giải:
Nếu $m-1=0$ thì $(d): y=2$
Khoảng cách từ $O$ đến đường thằng $y=2$ là $2$
Nếu $m-1\neq 0$
Gọi $A,B$ lần lượt là giao của $(d)$ với trục hoành và trục tung.
$y_A=0\Rightarrow x_A=\frac{y_A-2m}{m-1}=\frac{-2m}{m-1}$
$x_B=0\Rightarrow y_B=(m-1)x_B+2m=2m$
$\Rightarrow OA=|x_A|=|\frac{2m}{m-1}|; OB=|y_B|=|2m|$
Gọi khoảng cách từ $O$ đến $(d)$ là $h$ thì theo công thức hệ thức lượng trong tam giác vuông tại có:
$\frac{1}{h^2}=\frac{1}{OA^2}+\frac{1}{OB^2}=\frac{(m-1)^2}{(2m)^2}+\frac{1}{(2m)^2}=\frac{m^2-2m+2}{4m^2}$
$\Rightarrow h=\frac{2|m|}{\sqrt{m^2-2m+2}}$
Tổng kết 2 TH ta thấy khoảng cách từ $O$ đến $(d)$ là $h=\frac{2|m|}{\sqrt{m^2-2m+2}}$