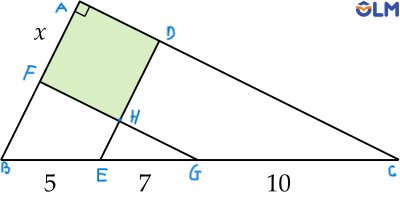
- Xét tam giác ABC có DE//AB:
-> Theo định lý Tales: DE/AB = EC/BC = 17/22
- Xét tam giác EDC có DH//HE:
-> Tương tự có DH/DE = 10/17
-> DH/AB = DH/DE x DE/AB = 5/11
-> AB = 11/5 x (*)
- Xét tam giác ABC có FG//AC:
-> Theo định lý Tales có: FG/AC = BG/BC = 6/11
- Xét tam giác BFG có HE//DB:
-> Tương tự, FH/FG = 5/12
-> FH/AC = FH/FG x FG/AC = 5/22
-> AC = 22/5 x (**)
Theo định lý Pythagoras và (*), (**):
AC^2 + AB^2 = BC^2
\(\left(\dfrac{11}{5}x\right)^2+\left(\dfrac{22}{5}x\right)^2=22^2\)
\(\left(\dfrac{121}{25}+\dfrac{484}{25}\right)x^2=484\)
\(\dfrac{121}{5}x^2=484
\)
\(x^2=20\)
Diện tích hình vuông = x^2 = 20 (đvdt)









