g 2cm. Vẽ ảnh AB.

Trả lời:

• Vật AB đặt vuông góc với gương phẳng, điểm A sát gương, điểm B cách gương 2cm.
• Cách vẽ ảnh:
• 1. Vẽ gương phẳng (một đường thẳng).
  2. Vẽ vật AB vuông góc với gương, B cách gương 2cm.
  3. Ảnh của AB là A'B', nằm phía sau gương, vuông góc với gương.
  4. Khoảng cách từ A' đến gương bằng khoảng cách từ A đến gương (nếu A sát gương thì A' cũng sát gương).
  5. Khoảng cách từ B' đến gương bằng khoảng cách từ B đến gương (2cm).

Kết luận:

• Ảnh A'B' vuông góc với gương, cùng chiều với AB, phía sau gương.
• Độ dài ảnh bằng độ dài vật.
• Khoảng cách từ mỗi điểm của ảnh đến gương bằng khoảng cách từ điểm tương ứng của vật đến gương.

Bỏ con

mình kiếm bài mẫu cho bạn thôi nhé:

Trọng lượng của nhà du hành vũ trụ trên Trái Đất là:

75,5 . 10 = 755 (N)

Trọng lượng của nhà du hành vũ trụ trên Mặt Trăng là:

755.16=7556≈125,83755  .  16=7556≈125,83 (N)

Vậy trọng lượng của nhà du hành vũ trụ trên Mặt Trăng là 125,83 N.

Câu trả lời:

a) Khi hai gương phẳng đặt vuông góc với nhau (90∘), một điểm sáng S giữa hai gương sẽ tạo ra 3 ảnh. Đây là do:

1. Một ảnh xuất hiện trên mỗi gương do ánh sáng phản xạ trực tiếp.
2. Một ảnh xuất hiện do phản xạ kép, ánh sáng từ S phản xạ lần lượt trên cả hai gương.

Vậy tổng cộng có 3 ảnh được tạo ra.

b) Khi hai gương phẳng G1 và G2 đặt song song, tia sáng tới SI phản xạ lần lượt trên G1 và G2. Để tính góc tạo bởi tia tới SI và tia phản xạ cuối cùng trên G2, ta sử dụng các nguyên tắc quang học:

1. Góc phản xạ bằng góc tới.
2. Góc tới trên G1 bằng góc phản xạ khỏi G1, tương tự với G2.

Do đó, tổng góc giữa tia tới SI ban đầu và tia phản xạ cuối cùng được tính dựa trên hình học của các gương.

khoảng cách từ người đó đến vách núi là 680 m. 😊

Tick cho mình

Chiều dài của lò xo khi không treo vật là 16 cm

Để giải bài toán này, ta cần tính thời gian xe A đi từ A đến G, sau đó dùng thời gian này để tính vận tốc cần thiết của xe B trong hai trường hợp.

1. Thời gian xe A đi từ A đến G:
2. • Quãng đường AG = 120 km
   • Vận tốc xe A = 50 km/h
   • Thời gian xe A đi từ A đến G: \(t_{A}=\frac{A G}{v_{A}}=\frac{120}{50}=2.4\text{ gi}ờ\)
3. Trường hợp a: Chuyển động cùng chiều
4. • Quãng đường BG = 96 km
   • Thời gian xe B cần để đi từ B đến G: \(t_{B}=t_{A}=2.4\text{ gi}ờ\)
   • Vận tốc xe B cần thiết: \(v_{B}=\frac{B G}{t_{B}}=\frac{96}{2.4}=40\text{ km}/\text{h}\)
5. Trường hợp b: Chuyển động ngược chiều
6. • Quãng đường BG = 96 km
   • Thời gian xe B cần để đi từ B đến G: \(t_{B}=t_{A}=2.4\text{ gi}ờ\)
   • Vận tốc xe B cần thiết: \(v_{B}=\frac{B G}{t_{B}}=\frac{96}{2.4}=40\text{ km}/\text{h}\)

Vậy, trong cả hai trường hợp, vận tốc cần thiết của xe B để gặp xe A tại điểm G cùng một lúc là 40 km/h.

a; chuyển động cùng chiều: 

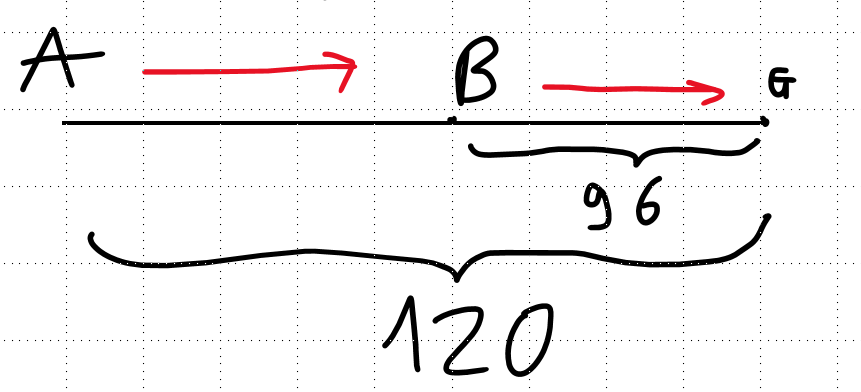
đoạn đường AB là: \(s_{AB}=s_{AG}-s_{BG}=120-96=24\left(km\right)\)

Thời gian ô tô đi từ A đến chỗ gặp là: \(t_A=\dfrac{s_{AG}}{v_A}=\dfrac{120}{50}=2,4\left(giờ\right)\)

Quãng đường xe đi từ A đến chỗ gặp cách A là: \(s_A=v_1t=50t\left(1\right)\)

Quãng đường xe đi từ B đến chỗ gặp cách A là: \(s_B=v_2t+24\left(2\right)\)

Từ (1) (2) ⇒ \(50\cdot2,4=v_2\cdot2,4+24⇒\:v_2=40\left(km\text{/}h\right)\)

b; chuyển động ngược chiều:

Thời gian xe A đi đến chỗ gặp là: \(t_A=\dfrac{s_{AG}}{v_{AG}}=\dfrac{120}{50}=2,4\left(\text{giờ}\right)\) (4)

Thời gian xe B đi đến chỗ gặp là: \(t_B=\dfrac{s_{BG}}{v_{BG}}=\dfrac{96}{v_{BG}}\left(3\right)\)

Mà thời gian đi đến chỗ gặp là bằng nhau nên từ (3) (4) ta có

\(\dfrac{96}{v_{BG}}=2,4⇒\:v_{BG}=40\left(km\text{/}h\right)\)

vậy: .....

an nèeee

5. Phân tích sự chuyển hóa về lực

Trả lời:
Sự chuyển hóa về lực là quá trình lực này sinh ra hoặc biến đổi thành lực khác thông qua các tương tác vật lý. Ví dụ, khi bạn kéo một vật bằng dây, lực kéo của bạn truyền qua dây tạo thành lực căng dây, lực này lại tác dụng lên vật làm vật chuyển động. Trong máy móc, lực do động cơ tạo ra có thể chuyển hóa thành lực ma sát, lực đàn hồi, hoặc lực nâng, tùy vào cơ cấu truyền lực. Sự chuyển hóa này tuân theo định luật bảo toàn năng lượng: lực không tự sinh ra hoặc mất đi mà chỉ chuyển từ dạng này sang dạng khác hoặc từ vật này sang vật khác.

Khi thả viên bi làm nó chuyển động->Tạo ra thế năng(từ trên cầu tuột xuống) rồi thành động năng và nhiệt năng (lực ma sát giữa viên bi và cầu tuột).