tính a,N=(1-1/22).(1-1/32)...(1-1/102)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
22 tháng 6 2023
\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{99}}\)
\(\Rightarrow\dfrac{A}{3}=\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\)
\(\Rightarrow A-\dfrac{A}{3}=\dfrac{2A}{3}=\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}\right)-\left(\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\dfrac{2A}{3}=\left(\dfrac{1}{3^2}-\dfrac{1}{3^2}\right)+\left(\dfrac{1}{3^3}-\dfrac{1}{3^3}\right)+...+\left(\dfrac{1}{3^{99}}-\dfrac{1}{3^{99}}\right)+\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)=\dfrac{1}{3}-\dfrac{1}{3^{100}}\)
\(\Rightarrow2A=3\cdot\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\text{A}=\dfrac{1-\dfrac{1}{3^{99}}}{2}\)
\(\Rightarrow A=\dfrac{1}{2}-\dfrac{1}{2.3^{99}}< \dfrac{1}{2}\)
TB
2
6 tháng 3 2023
Ta thấy \(\dfrac{1}{2^2}< \dfrac{1}{1.2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2.3}\)
......
\(\dfrac{1}{10^2}< \dfrac{1}{9.10}\)
hay \(D=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+....+\dfrac{1}{10^2}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{9.10}\)
\(D< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+....+\dfrac{1}{9}-\dfrac{1}{10}\)
\(D< 1-\dfrac{1}{10}=\dfrac{9}{10}< 1\) ( đpcm )
6 tháng 3 2023
Ta có \(\dfrac{1}{2.2}\) < \(\dfrac{1}{1.2}\)
\(\dfrac{1}{3.3}\)<\(\dfrac{1}{2.3}\)
\(\dfrac{1}{4.4}\)<\(\dfrac{1}{3.4}\)
.........................
\(\dfrac{1}{10.10}\)<\(\dfrac{1}{9.10}\)
=>\(\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{10.10}\)\(< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{9.10}\)
=> D < 1 - \(\dfrac{1}{10}\)
=>D < \(\dfrac{9}{10}\)
=> D < \(\dfrac{10}{10}\)
Vậy D < 1
TS
3
22 tháng 8 2023
\(B=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{10^2}\)
\(\dfrac{1}{2^2}< \dfrac{1}{1.2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2.3}\)
\(.....\)
\(\dfrac{1}{10^2}< \dfrac{1}{9.10}\)
\(\Rightarrow B=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{10^2}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{9.10}\)
\(\Rightarrow B=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{10^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}=1-\dfrac{1}{10}< 1\)
\(\Rightarrow B< 1\left(dpcm\right)\)
22 tháng 8 2023
\(B=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{10^2}\)
\(B< \dfrac{1}{1\times2}+\dfrac{1}{2\times3}+...+\dfrac{1}{9\times10}\)
\(B< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
\(B< 1-\dfrac{1}{10}\)
\(B< \dfrac{9}{10}< 1\)
Vậy \(B< 1\)
9 tháng 7 2023
A=1/2^2+1/3^2+...+1/10^2
=>A<1-1/2+1/2-1/3+...+1/9-1/10=1-1/10<1
PT
1
11 tháng 2 2021
a) uses crt;
var n,x,i:longint;
lt:real;
begin
clrscr;
write('Nhap co so n=');readln(n);
write('Nhap so mu x='); readln(x);
lt:=1;
for i:=1 to x do
lt:=lt*n;
writeln(n,'^',x,'=',lt:0:0);
readln;
end.
13 tháng 11 2023
\(B=1\cdot2\cdot3+2\cdot3\cdot4+...+\left(n-1\right)\cdot n\cdot\left(n+1\right)\)
=>\(4B=1\cdot2\cdot3\cdot4+2\cdot3\cdot4\cdot4+...+\left(n-1\right)\cdot n\left(n+1\right)\cdot4\)
=>\(4B=1\cdot2\cdot3\cdot4+2\cdot3\cdot4\left(5-1\right)+...+\left(n-1\right)\cdot n\left(n+1\right)\left[\left(n+2\right)-\left(n-2\right)\right]\)
=>\(4B=1\cdot2\cdot3\cdot4-1\cdot2\cdot3\cdot4+...+\left(n-2\right)\left(n-1\right)\cdot n\cdot\left(n+1\right)-\left(n-2\right)\cdot\left(n-1\right)\cdot n\cdot\left(n+1\right)+\left(n-1\right)\cdot n\left(n+1\right)\left(n+2\right)\)
=>\(4B=\left(n-1\right)\cdot n\cdot\left(n+1\right)\left(n+2\right)\)
=>\(B=\dfrac{\left(n-1\right)\cdot n\left(n+1\right)\left(n+2\right)}{4}\)
\(C=1\cdot4+2\cdot5+3\cdot6+...+n\left(n+3\right)\)
\(=1\cdot\left(1+3\right)+2\left(2+3\right)+...+n\left(n+3\right)\)
\(=\left(1^2+2^2+...+n^2\right)+3\left(1+2+...+n\right)\)
\(=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}+3\cdot\dfrac{n\left(n+1\right)}{2}\)
\(=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}+\dfrac{3n\left(n+1\right)}{2}\)
\(=\dfrac{n\left(n+1\right)}{2}\cdot\left(\dfrac{2n+1}{3}+3\right)\)
\(=\dfrac{n\left(n+1\right)}{2}\cdot\dfrac{2n+1+9}{3}\)
\(=\dfrac{n\left(n+1\right)\left(n+5\right)}{3}\)
\(D=1^2+2^2+...+n^2\)
\(=1+\left(1+1\right)\cdot2+\left(1+2\right)\cdot3+...+\left(1+n-1\right)\cdot n\)
\(=1+2+3+...+n+\left(1\cdot2+2\cdot3+...+\left(n-1\right)\cdot n\right)\)
Đặt \(A=1+2+3+...+n;E=1\cdot2+2\cdot3+...+\left(n-1\right)\cdot n\)
\(E=1\cdot2+2\cdot3+...+\left(n-1\right)\cdot n\)
=>\(3E=1\cdot2\cdot3+2\cdot3\cdot3+...+\left(n-1\right)\cdot n\cdot3\)
=>\(3E=1\cdot2\cdot3+2\cdot3\cdot\left(4-1\right)+...+\left(n-1\right)\cdot n\left[\left(n+1\right)-\left(n-2\right)\right]\)
=>\(3E=1\cdot2\cdot3-1\cdot2\cdot3+2\cdot3\cdot4+...+\left(n-1\right)\cdot n\left(n-2\right)-\left(n-1\right)\cdot n\left(n-2\right)+\left(n-1\right)\cdot n\cdot\left(n+1\right)\)
=>\(3E=\left(n-1\right)\cdot n\left(n+1\right)=n^3-n\)
=>\(E=\dfrac{n^3-n}{3}\)
\(A=1+2+3+...+n\)
Số số hạng là n-1+1=n(số)
Tổng của dãy số là: \(A=\dfrac{n\left(n+1\right)}{2}\)
=>\(D=\dfrac{n^3-n}{3}+\dfrac{n\left(n+1\right)}{2}\)
\(=\dfrac{2n^3-2n+3n^2+3n}{6}\)
=>\(D=\dfrac{2n^3+3n^2+n}{6}\)
13 tháng 4 2018
phần a dễ bạn tự làm đi tử thì bạn tính như bình thường còn mẫu thì:7.(\(\frac{1}{3.13}\)+\(\frac{1}{13.23}\)+\(\frac{1}{23.33}\))
\(\frac{7}{10}\).(\(\frac{1}{3}\)-\(\frac{1}{33}\))=\(\frac{7}{33}\)
b)(1+1/3+1/5+..+1/199)-(1/2+1/4+...+1/200)
(1+1/2+1/3+...+1/199+1/200)-(1/2+1/2+1/4+1/4+...+1/200+1/200)
=1+1/2+1/3+...+1/199+1/200-(1+1/2+1/3+...+1/100)
=1/101+1/102+...+1/200
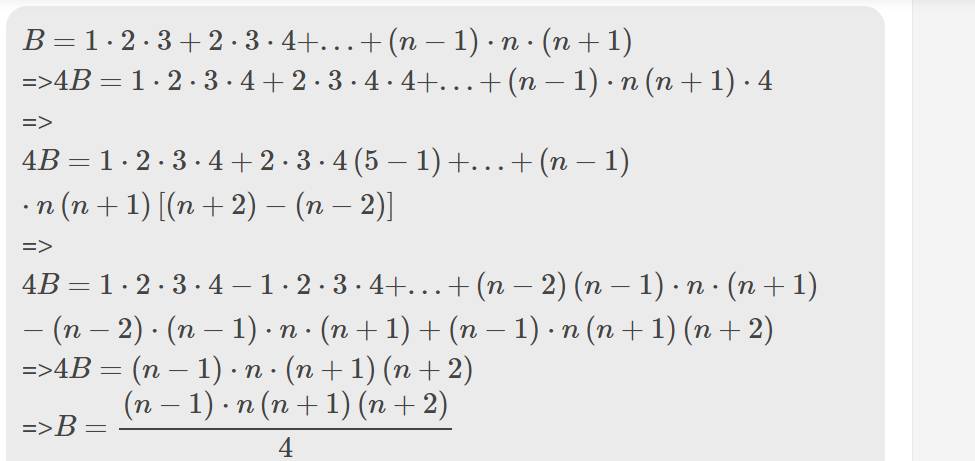
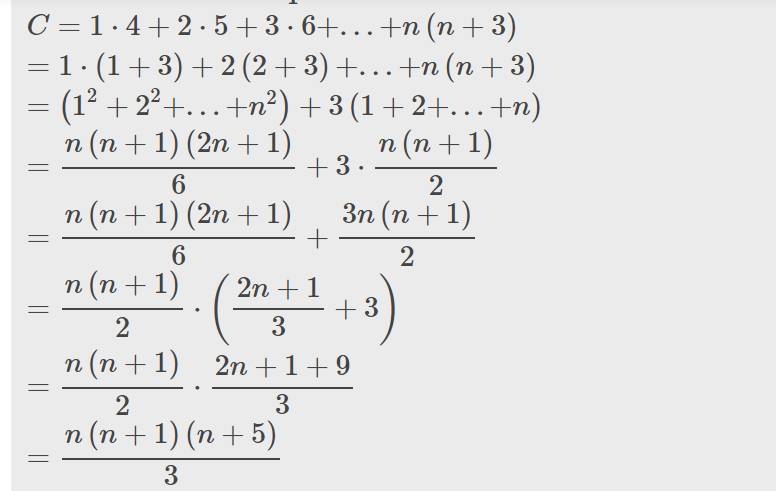
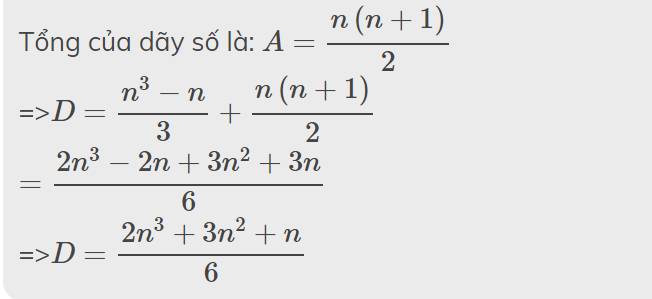
N=\(\left(1-\frac{1}{2^2}\right)\left(1-\frac{1}{3^2}\right)...\left(1-\frac{1}{10^2}\right)\)
= \(\frac{1.3}{2^2}.\frac{2.4}{3^2}...\frac{8.10}{9^2}\)
= \(\frac{1.2.3...8}{2.3...9}.\frac{3...8.9.10}{2.3...9}\)
=\(\frac{1}{9}.\frac{10}{2}\)
= \(\frac{1}{9}.5=\frac{5}{9}\)