cho hình thang ABCD(AB//CD) có S=36cm vuông. AB=4cm CD=8cm .O là gđ 2 đg chéo.Tính Stam giác COD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 6 2018
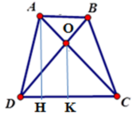
Kẻ AH ⊥ DC; OK ⊥ DC tại H, K suy ra AH // OK
Chiều cao của hình thang: AH = 2 S A B C D A B + C D = 2.48 4 + 8 = 8 (cm)
Vì AB // CD (do ABCD là hình thang) nên theo định lý Ta-lét ta có
O C O A = C D A B = 8 4 = 2 ⇒ O C O A + O C = 2 2 + 1 ⇒ O C A C = 2 3
Vì AH // OK (cmt) nên theo định lý Ta-lét cho tam giác AHC ta có:
O K A H = O C A C = 2 3 => OK = 2 3 AH => OK = 2 3 .6 = 4(cm)
Do đó S C O D = 1 2 OK.DC = 1 2 . 16 3 .8 = 64 3 c m 2
Đáp án: A
CM
12 tháng 5 2017
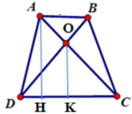
Kẻ AH ⊥ DC; OK ⊥ DC tại H, K suy ra AH // OK
Chiều cao của hình thang: AH = 2 S A B C D A B + C D = 2.36 4 + 8 = 6 (cm)
Vì AB // CD (do ABCD là hình thang) nên theo định lý Ta-lét ta có
O C O A = C D A B = 8 4 = 2 ⇒ O C O A + O C = 2 2 + 1 ⇒ O C A C = 2 3
Vì AH // OK (cmt) nên theo định lý Ta-lét cho tam giác AHC ta có:
O K A H = O C A C = 2 3 => OK = 2 3 AH => OK = 2 3 .6 = 4(cm)
Do đó S C O D = 1 2 OK.DC = 1 2 .4.8 = 16cm2
Đáp án: C
14 tháng 2 2022
b) -Xét △AOH có: AB//CD (gt).
\(\Rightarrow\dfrac{AO}{OC}=\dfrac{OH}{OK}\) (định lí Ta-let).
\(\Rightarrow\dfrac{OH}{OK}=\dfrac{4}{8}=\dfrac{1}{2}\).
c) -Xét △ADC có: OE//DC (gt).
\(\Rightarrow\dfrac{AE}{AD}=\dfrac{AO}{AC}\) (định lí Ta-let).
-Xét △ABC có: OF//AB (gt).
\(\Rightarrow\dfrac{AO}{AC}=\dfrac{BF}{BC}\) (định lí Ta-let).
Mà \(\dfrac{AE}{AD}=\dfrac{AO}{AC}\) nên \(\dfrac{AE}{AD}=\dfrac{BF}{BC}\)
\(\Rightarrow\dfrac{AE}{AD}+\dfrac{CF}{BC}=\dfrac{BF}{BC}+\dfrac{CF}{BC}=\dfrac{BC}{BC}=1\)