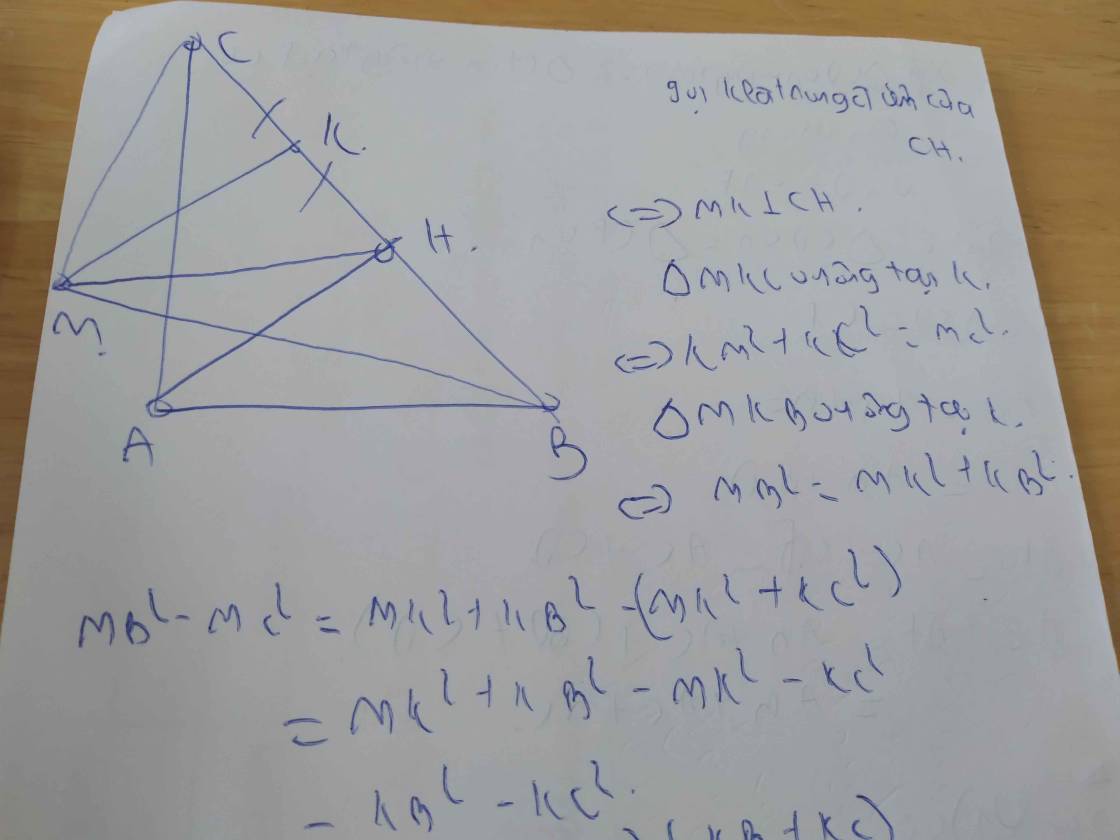
Cho tam giác ABC vuông cân tại A. Trên BC lấy điểm M. Tìm GTNN của MA2+MB2+MC2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Gọi O là tâm đường tròn ngoại tiếp. Do tam giác ABC là tam giác đều nên O đồng thời là trọng tâm tam giác đều ABC.
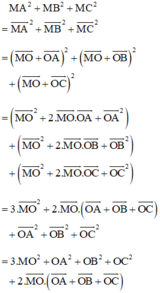
Lại có:
+ O là trọng tâm tam giác nên 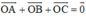
+ Bán kính đường tròn ngoại tiếp tam giác:
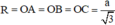
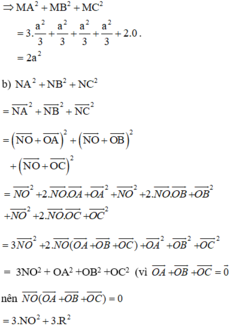
Ta có: NA2 + NB2 + NC2 ngắn nhất
⇔ NO2 ngắn nhất vì R không đổi
⇔ NO ngắn nhất
⇔ N là hình chiếu của O trên d.

a, Gọi I là trọng tâm của ΔABC
⇒ \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\)
MA2 + MB2 + MC2 = k2
⇔ 3MI2 + 2\(\overrightarrow{MI}\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}\right)+AB^2+AC^2+BC^2\) = k2
⇔ 3MI2 = k2 - 1014
⇔ MI = \(\sqrt{\dfrac{k-1014}{3}}\) = const
Vậy M thuộc \(\left(I;\sqrt{\dfrac{k-1014}{3}}\right)\)

Đáp án C.
Gắn hệ trục tọa độ Oxyz, với O(0;0;0) là trung điểm của AB => OC= 3
Khi đó
![]()
![]()
![]()
![]()
⇒ x 2 + ( y + 1 ) 2 + z 2 + x 2 + ( y - 1 ) 2 + z 2 + 2 ( x - 3 ) 2 + 2 y 2 + 2 z 2 = 12
![]()
![]()
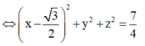
Vậy tập hợp các điểm M là một mặt cầu có bán kính
R
=
7
2

Chọn A
Gọi là trọng tâm tam giác ABC. Suy ra: G(2;-2;2)
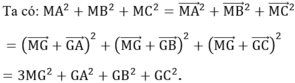
Do tổng GA2 + GB2 + GC2 không đổi nên MA2 + MB2 + MC2 đạt giá trị nhỏ nhất khi và chỉ khi GM2 nhỏ nhất
Mà S nằm trên mặt phẳng (Oyz) nên M là hình chiếu vuông góc của G lên mặt phẳng (Oyz). Suy ra: M(0;-2;2)
Vậy P = x+y+z = 0 + (-2) + 2 = 0

Gọi M(x, y)
⇒ MA2 = (x – 1)2 + (y – 2)2
MB2 = (x + 3)2 + (y – 1)2
MC2 = (x – 4)2 + (y + 2)2
MA2 + MB2 = MC2
⇔ (x – 1)2 + (y – 2)2 + (x + 3)2 + (y – 1)2 = (x – 4)2 + (y + 2)2
⇔ [(x – 1)2 + (x + 3)2 – (x – 4)2] + [(y – 2)2 + (y – 1)2 – (y + 2)2] = 0
⇔ (x2 – 2x +1 +x2 + 6x + 9 – x2 + 8x -16) + (y2 – 4y + 4 + y2 – 2y + 1 – y2 – 4y – 4) = 0
⇔ (x2 + 12x – 6) + (y2 – 10y + 1) = 0
⇔ (x2 + 12x – 6 +42) + (y2 – 10y + 1+ 24) = 42 +24
⇔ (x2 + 12x + 36) + (y2 – 10y + 25) = 66
⇔ (x + 6)2 + (y – 5)2 = 66.
Vậy tập hợp các điểm M là đường tròn tâm I(–6; 5), bán kính R = √66.