Nêu cách tìm nghiệm \(a^3-a^2.b+a.b^2-6b^3\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 12 2016
Gọi a = 125 . k ; b = 125 . h thì (k ; h) = 1 và k ; h \(\in\)N*
Ta có a . b = 125 . k . 125 . h = 93750
125 . 125 . k . h = 93750
15625 . k . h = 93750
k . h = 93750 : 15625
k . h = 6
Ta có bảng sau :
| k | 6 | 3 |
| h | 1 | 2 |
| a = 125.k | 750 | 375 |
| b = 125.h | 125 | 250 |
Vậy ta có các bộ số (a, b) là : (750, 125) ; (375, 250)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
31 tháng 7 2023
1)
a.b=42 => a,b ∈ Ư(42)= {1;2;3;6;7;14;21;42}
a,b là 2 số tự nhiên và a.b=42 => (a;b)= (6;7) (Nhận) ; (a;b)= (7;6) (Loại)
=> a=6;b=7
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
31 tháng 7 2023
2)
a.b=30 => a;b ∈ Ư(30)= {1;2;3;5;6;10;15;30}
Các cặp ban đầu (1;30) loại; (2;15) loại; (3;10) loại; (5;6) nhận
Vì: a < b => a=5;b=6
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
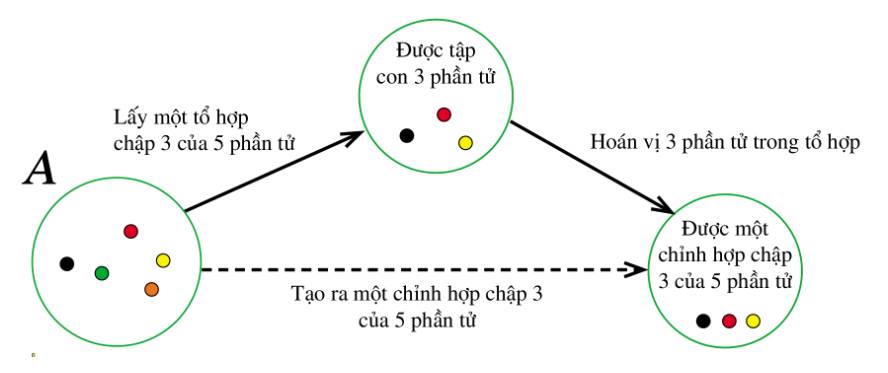
a) Cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A là: Chọn bất kỳ 3 trong 5 phần tử thuộc A ví dụ như \(\left\{ {a;b;c} \right\}\)
b) Cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A là: Chọn bất kỳ 3 trong 5 phần tử thuộc A rồi sắp xếp theo một thứ tự nào ví dụ như ta chọn 3 phần tử a,b,c rồi sắp xếp theo thứ tự ngược của bảng chữ cái \(\left\{ {c;b;a} \right\}\)
c) So sánh: Mỗi tổ hợp chập 3 của 5 phần tử sinh ra 3! chỉnh hợp chập 3 của 5 phần tử vì có 3! hoán vị của 3 phần tử. Vì thế, số chỉnh hợp chập 3 của 5 phần tử nhiều gấp 3! lần số tổ hợp chập 3 của 5 phần tử.
8 tháng 4 2022
Bài 3:
\(\text{Δ}=1^2-4\cdot2\cdot\left(-4m-2\right)\)
=1+8(4m-2)
=32m-16+1=32m-15
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>32m-15>0
hay m>15/32
Để phương trình vô nghiệm thì 32m-15<0
hay m<15/32
Để phương trình có nghiệm kép thì 32m-15=0
hay m=15/32
5 tháng 7 2020
Bài làm
1. thu gọn đa thức:
a. A(x) = x3 + x2 - 5x + 1
Thu gọn rồi nhé.
b. B(x)= -x + 4x2 - x3 -3x2 + 5
Thu gọn luôn rồi :v
Tính A(x)+B(x), tính A(x)- B(x)
A(x) + B(x) = x3 + x2 - 5x + 1 + (-x) + 4x2 - x3 -3x2 + 5
= x3 + x2 - 5x + 1 - x + 4x2 - x3 - 3x2 + 5
= ( x3 - x3 ) + ( x2 + 4x2 - 3x2 ) + ( -5x - x ) + ( 1 + 5 )
= 2x2 - 6x + 6
Vậy A(x) + B(x) = 2x2 - 6x + 6
A(x) - B(x) = x3 + x2 - 5x + 1 - [(-x) + 4x2 - x3 -3x2 + 5]
= x3 + x2 - 5x + 1 + x - 4x2 + x3 + 3x2 - 5
= ( x3 + x3 ) + ( x2 - 4x2 + 3x2 ) + ( -5x + x ) + ( 1 - 5 )
= 2x3 - 4x - 4
Vậy A(x) - B(x) = 2x3 - 4x - 4
b. Tìm x để A(x)- B(x)=0
Để A(x) - B(x) = 0
<=> 2x3 - 4x - 4 = 0
Tự giải tiếp ra nhé. Bài dài mà mình lười. thông cảm :L
2. cho A= 5x3y2, B= −15xy3z
a. tính A.B
A . B = ( 5x3y2 ) . ( -15xy3z )
A . B = -75x4y5z
Vậy A . B = -75x4y5z
b. tìm bậc của A.B
Bậc của A . B là 10
3. tìm nghiệm các đa thức:
a. A(x) = x2 - x
Để đa thức A(x) có nghiệm thì:
x2 - x = 0
=> x( x - 1 ) = 0
=> x = 0 hoặc x - 1 = 0
=> x = 0 hoặc x = 1
Vậy x = 0 hoặc x = 1 là nghiệm của đa thức A(x)
b.B(x) = x2 - 1
Để đa thức B(x) có nghiệm thì:
x2 - 1 = 0
=> x2 = 1
=> x = + 1
Vậy x = + 1 là nghiệm của đa thức B(x)
c.C(x) = x2 + 1
Để đa thức C(x) có nghiệm thì:
x2 + 1 = 0
=> x2 = -1 ( vô lí )
Vậy đa thức trên không có nghiệm.
d.D(x) = x3 - x
Để đa thức D(x) có nghiệm thì:
x3 - x = 0
=> x( x2 - 1 ) = 0
=> x = 0 hoặc x2 - 1 = 0
=> x = 0 hoặc x2 = 1
=> x = 0 hoặc x = + 1
Vậy x = 0 hoặc x = + 1 là nghiệm của đa thức D(x)
6 tháng 11 2016
Gọi hai số cần tìm là a;b
-Ta có:BCNN (a;b)=ab
=>ƯCLN(a;b)=ab;BCNN(a,b)=4320:360=12
-Gọi a=12m
b=12n(ƯCLN(m;n)=1
=>ab=12m.12n=4320
=>144mn=4320
=>mn=30
Ta tìm được (m;n)=(1;30) (2;15) (3;10) (5;6) (6;5) (10;3) (15;2) (30;1)
Lấy m;n nhân với 12,ta tim được (a;b)=(12;360) (14;180) (36;120) (60;72) (72;60) (120;36) (180;14) (360;12)
30 tháng 6 2019
1.
\(ƯCLN\left(a,b\right)=7\)
\(\Rightarrow a,b\)chia hết cho 7
\(\Rightarrow a,b\in B\left(7\right)\)
\(B\left(7\right)=\left(0;7;14;21;28;35;42;49;56;63;70;77;84;91;98;105...\right)\)
a, vì a+b=56 \(\Rightarrow\)\(a\le56;b\le56\)
\(\Rightarrow a=56;b=0.a=0;b=56\)
\(a=7;b=49.a=49;b=7\)
\(a=14;b=42.a=42;b=14\)
\(a=21;b=35.a=35;b=21\)
\(a=b=28\)
b, a.b=490 \(\Rightarrow a< 490;b< 490\)
\(\Rightarrow\) \(a=7;b=70-a=70;b=7\)
\(a=14;b=35-a=35;b=14\)
c, BCNN (a,b) = 735
\(\Rightarrow a,b\inƯ\left(735\right)\)
\(Ư\left(735\right)=\left(1;3;5;7;15;21;35;49;105;147;245;735\right)\)
\(\Rightarrow\)\(a=7;b=105-a=105;b=7\)
2.
a+b=27\(\Rightarrow\)\(a\le27;b\le27\)
ƯCLN(a,b)=3
\(\Rightarrow a,b\in B\left(_{ }3\right)\in\left(0;3;6;9;12;15;18;21;24;27;30;...\right)\)
BCNN(a,b)=60
\(\Rightarrow a,b\inƯ\left(60\right)\in\left(1;2;3;4;5;6;10;12;15;20;60\right)\)
\(\Rightarrow\)\(a=12;b=15-a=15;b=12\)