Cho điểm \(A\)nằm ngoài đường tròn \(\left(O;R\right)\). Từ \(A\)kẻ đường thẳng \(d\)ko đi qua tâm \(O\), cắt đường tròn \(\left(O\right)\)tại \(B\)và \(C\)( \(B\)nằm giữa \(A\)và \(C\)). Các tiếp tuyến với đường tròn \(\left(O\right)\)tại \(B\)và \(C\)cắt nhau tại \(D\). Từ \(D\)kẻ \(DH\perp AO\)( \(H\in AO\)), \(DH\)cắt cung nhỏ \(BC\)tại \(M\)
a) \(CM\)4 điểm \(O,H,D,C\) cùng thuộc 1 đường tròn
b) gọi \(I\)là giao điểm của \(DO,BC\). \(Cm\)\(OH.OA=OI.OD\)
C) \(CM\)\(AM\) là tiếp tuyến của đường tròn \(\left(O\right)\)

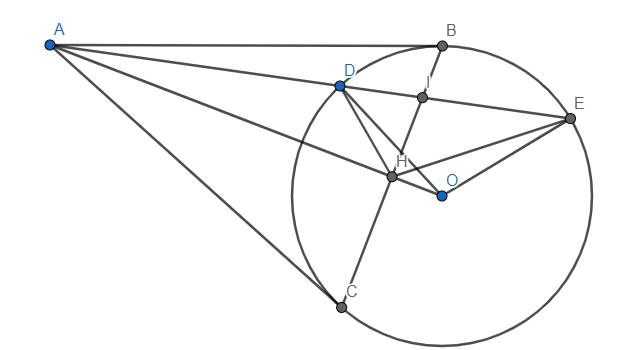



O A C B D H I M
a) Tam giác COD và HOD là các tam giác vuông có chung cạnh huyền OD nên O, H, D, C cùng thuộc đường tròn đường kính OD.
b) Theo tính chất hai tiếp tuyến cắt nhau, ta có \(OD\perp BC\)
Tam giác DIA và DHA là hai tam giác vuông có chung cạnh AD nên DIHA là tứ giác nội tiếp.
Vậy thì \(\widehat{IDA}=\widehat{IHO}\)
Từ đó ta có \(\Delta IOH\sim\Delta AOD\left(g-g\right)\Rightarrow\frac{OI}{OA}=\frac{OH}{OD}\Rightarrow OH.OA=OI.OD\)
c) Xét tam giác vuông DBO, chiều cao BI, ta có:
\(OI.OD=OB^2\) (Hệ thức lượng)
Mà \(OB^2=OM^2;OI.OD=OH.OA\Rightarrow OM^2=OH.OA\)
\(\Rightarrow\Delta OHM\sim\Delta OMA\left(c-g-c\right)\Rightarrow\widehat{OMA}=\widehat{OHM}=90^o\)
Vậy AM là tiếp tuyến của đường tròn (O).