Question

[Mafia]

cho đường tròn \(\left(O;\frac{AB}{2}\right)\)và \(AB=10cm\). C là điểm \(\in\)đường tròn tâm \(\left(O\right)\)sao cho \(AC=6cm\). Vẽ \(CH\perp AB\)   \(\left(H\in AB\right)\)

a) \(CH=?\),  \(\widehat{ABC}=?\)  ( làm tròn)

b) tiếp tuyến tại \(B\)và   \(C\)   của đường tròn \(\left(O\right)\)cắt nhau ở \(D\)

\(CMR\)\(OD\perp BC\)

c) tiếp tuyến tại  \(A\)  của đường tròn \(\left(O\right)\)cắt \(BC\)ở \(E\). \(CMR\)\(CE.CB=AH.AB\)

D) gọi \(I\)là trung điểm của \(CH\), tia \(BI\)cắt \(AE\)ở \(F\)

\(CMR:FC\)là tiếp tuyến của đường tròn \(\left(O\right)\)

Answer 1

[Cô Hoàng Huyền]

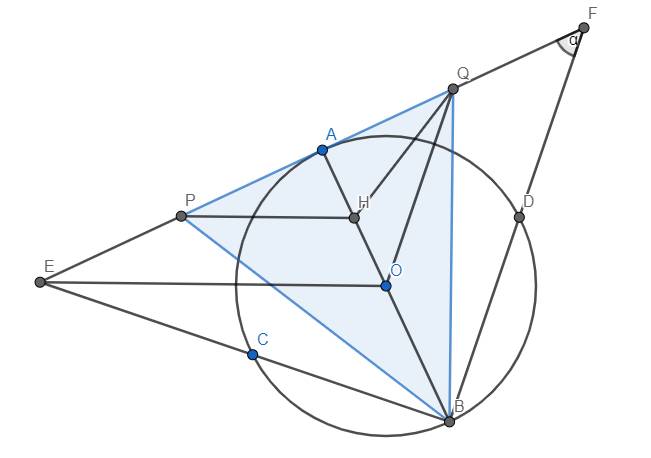
A B O C H D E F

a) Do C thuộc đường tròn nên \(\widehat{ACB}=90^o\)

Áp dụng định lý Pi-ta-go: \(BC=\sqrt{10^2-6^2}=8\left(cm\right)\)

Xét tam giác vuông ACB, đường cao CH. Áp dụng hệ thức lượng trong tam giác, ta có:

\(CH.AB=CA.BC\Rightarrow CH=\frac{6.8}{10}=4,8\left(cm\right)\)

Ta thấy \(sin\widehat{ABC}=\frac{AC}{AB}=\frac{6}{10}\Rightarrow\widehat{ABC}\approx36^o52'\)

b) Theo tính chất hai tiếp tuyến cắt nhau, ta có: \(DC=DB\) và DO là phân giác góc BDC.

Vậy thì DO cũng là đường trung trực của BC hay \(DO\perp BC.\)

c) Xét tam giác vuông ABC, đường cao CH, ta có : \(AH.AB=AC^2\) (Hệ thức lượng)

Xét tam giác vuông AEB, đường cao AC, ta có: \(AC^2=EC.CB\) (Hệ thức lượng)

Vậy nên \(AH.AB=EC.CB\)

d) Ta thấy HC // AE (Cùng vuông góc với AB)

Áp dụng Ta let ta có: \(\frac{IH}{AF}=\frac{IC}{EF}\left(=\frac{IB}{FB}\right)\)

mà IH = IC nên AF = FE.

Xét tam giác vuông ACE có F là trung điểm cạnh huyền nên FA = FE = FC.

Xét tam giác FAO và FCO có: FO chung, FA = FC, AO = CO nên \(\Delta FAO=\Delta FCO\left(c-c-c\right)\) 

\(\Rightarrow\widehat{FCO}=\widehat{FAO}=90^o\)

Vậy nen FO là tiếp tuyến của đường tròn.