K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 9 2016
- Hai đường thẳng cùng thẳng góc với đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.
- Một đường thẳng cắt hai đường thẳng mà trong các góc tạo thành có các cặp góc: Đồng vị hay so le trong bằng nhau thì hai đường thẳng bị cắt là hai đường thẳng song song.
- Một đường thẳng cắt hai đường thẳng và định ra trên hai đường thẳng đó những đoạn thẳng tương ứng tỷ lệ bằng nhau, thì hai đường thẳng đó song song nhau.
- Hai đường thẳng cùng song song với một đường thẳng thứ ba, thì hai đường thẳng đó song song nhau.
6 tháng 9 2016
Hai đường thẳng song song là hai đường thẳng đối diện nhau
Ko có điểm chung nào
M
9 tháng 10 2019
TL :
a) Vẽ thêm các tia đối của các tia Dm, Cp, Bq và An.
Vẽ thêm các đường phân giác Ds và Ar của góc ∠D và ∠A.
Khi đó chứng minh được Cp song song với Ds.
Tương tự chứng minh được Ar song song với Dm.
Từ đó suy ra được: An // Cp và Dm // Bq.
b) Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.
Từ đó suy ra được: An vuông góc với Bq.
Hok tốt
LM
13 tháng 8 2016
a b c d O K m n g h
Ta có: ab // cd và \(\widehat{aOK}=\widehat{OKd}\)(2 góc so le trong)\(\Rightarrow\frac{1}{2}\widehat{aOK}=\frac{1}{2}\widehat{OKd}\)(1)
Mặt khác: Om là phân giác góc aOK =>\(\widehat{aOm}=\widehat{mOK}=\frac{1}{2}\widehat{aOK}\)(2)
On là phân giác góc OKd =>\(\widehat{nOK}=\widehat{nOd}=\frac{1}{2}\widehat{OKd}\)(3)
Từ (1);(2);(3)\(\Rightarrow\widehat{mOK}=\widehat{nOK}\)=> Om // Kn (2 góc so le trong bằng nhau)
Chứng minh tương tự ta cũng được Og // Oh
Vậy nếu 2 đường thẳng song song cắt 1 đường thẳng thứ 3 thì các tia phân giác của 2 góc so le trong song song với nhau.
TT
8 tháng 10 2017
Vì một đường thẳng cắt hai đường thẳng song song nên các góc sole trong bằng nhau
Vậy tia phân giác của 2 góc so le trong chia 2 góc đó mỗi góc làm 2 góc bằng nhau
Gọi hai góc chung cạnh kết hợp với tia phân giác tạo thành hai góc bằng nhau là A1 và B3
===> A1=B3=1/2 hai góc so le trong bằng nhau
Vậy chúng song song với nhau(đpcm)
Bút danh XXX
23 tháng 7 2015
Hỏi nhiều quá , mà thà bạn nói ko cần vẽ hình thì còn giải , đằng này đã vẽ hình còn phải ghi GT , KL . mệt !!!!!!!!!!! @_@
11 tháng 11 2016
Chứng Minh Định lý hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì chúng song song với nhau
HP
3
21 tháng 9 2016
x y z t a b A B xy // zt c 1 1
Aa,Bb lần lượt là phân giác của\(\widehat{yAB},\widehat{tAc}\)nên\(\widehat{A_1}=\frac{\widehat{yAB}}{2};\widehat{B_1}=\frac{\widehat{tAc}}{2}\)mà\(\widehat{yAB}=\widehat{tAc}\)(2 góc đồng vị của xy // zt)
\(\Rightarrow\widehat{A_1}=\widehat{B_1}\)(2 góc đồng vị bằng nhau) => Aa // Bb (đpcm)
18 tháng 9 2023
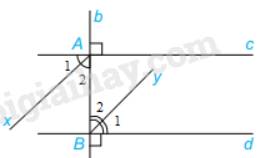
Vì Ax là tia phân giác của góc A vuông nên \(\widehat {{A_1}} = \widehat {{A_2}} = \frac{1}{2}.90^\circ = 45^\circ \)
Vì By là tia phân giác của góc B vuông nên \(\widehat {{B_1}} = \widehat {{B_2}} = \frac{1}{2}.90^\circ = 45^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{B_2}}( = 45^\circ )\), mà hai góc này ở vị trí so le trong nên Ax // By (Dấu hiệu nhận biết hai đường thẳng song song)
kẻ RH sao cho H đối diện với R qua O
ta có: ∠POH = 180⁰ - ∠ROP = 180⁰ - 110⁰ = 70⁰
∠NOH = 180⁰ - ∠RON = 180⁰ - 130⁰ = 50⁰
∠NOP = ∠POH + ∠NOH = 70⁰ + 50⁰ = 120⁰
⇒ ∠NOP = ∠OPQ = 120⁰
mà 2 góc này ở vị trí so le trong
⇒ PQ // NQ