K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GH
29 tháng 11 2023
hiệu khi không giảm số trừ đi 9 là:
55-9=46
hiệu ban đầu là:
46-14=32
Đ/s:32
KV
15 tháng 11 2023
Số tuổi mẹ tăng thêm kể từ khi sinh con:
42 - 27 = 15 (năm)
Số tuổi của con bằng số tuổi mẹ tăng thêm nên con 15 tuổi
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 11 2023
Kiến thức quan trọng cần nhớ với các bài toán về tuổi là hiệu số tuổi luôn không đổi theo thời gian em nhé
Giải
Vì mỗi năm mỗi người tăng thêm một tuổi nên hiệu số tuổi của hai mẹ con luôn không đổi theo thời gian.
Mẹ sinh con năm mẹ 27 tuổi vậy mẹ hơn con 27 tuổi, hiện nay mẹ vẫn hơn con 27 tuổi.
Từ những lập luận trên ta có:
Tuổi con hiện nay là: 42 - 27 = 15 (tuổi)
Đáp số: 15 tuổi.
3 tháng 4 2016
cách 1 cộng theo hàng ngang (cái này dễ nên bạn tự làm nhé)
cách 2 cộng theo hàng dọc sắp xếp theo lũy thừa giảm dần của biến rồi cộng trừ như cộng trừ số số hàng
3 tháng 4 2016
Cách 1 : cộng theo hàng ngang
Cách 2 : cộng theo hàng dọc ( đa số sử dụng cách này )
W
0
ND
14
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
11 tháng 1 2023
Theo quan sát hình vẽ thì thực tế đã có 6 cái ghế
Vì mỗi ghế để 1 người ngồi nên 6 ghế có 6 người ngồi
tất cả có 19 người vậy số người chưa có ghế là :
19 - 6 = 13 (người )
vì mỗi người một ghế nên số ghế cần thêm là 16 ghế.
Sau đây là bài giải chi tiết em nhé :
Số ghế cần thêm là : 19 - 6 = 13 ( ghế )
4 tháng 1 2024
Cân lần 1: Đặt quả cân 1kg lên một dĩa cân, đổ 13kg gạo vào hai dĩa cân cho đến khi cân thăng bằng. Vậy ta được một dĩa cân có 6kg và một dĩa cân có 7kg.
Cân lần 2: Đặt quả cân 1kg lên một dĩa cân, đổ 7kg vào hai dĩa cân cho đến khi cân thăng bằng. Vậy ta được một dĩa 3kg và một dĩa có 4kg. Như vậy ta đã cân được 4kg gạo
TT
26 tháng 10 2020
Nếu nhớ không nhầm thì hướng dẫn chi tiết cho rồi :vv
\(x^7+x^2+1=x\left(x^6-1\right)+\left(x^2+x+1\right)\)
\(=x\left(x^3-1\right)\left(x^3+1\right)+\left(x^2+x+1\right)\)
\(=x\left(x-1\right)\left(x+1\right)\left(x^2-x+1\right)\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left[\left(x^3-x\right)\left(x^2-x+1\right)+1\right]\)
P/s : ko chắc lém :)))
30 tháng 10 2017
60 = 5 . 3 . 22
280 = 5 . 7 . 23
=> ƯCLN ( 60 ; 280 ) = 5 . 22 = 20
B
1
12 tháng 9 2021
Ta có: \(\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}+\sqrt{\left(2-\sqrt{5}\right)^2}-2\sqrt{5}\)
\(=\sqrt{5}+\sqrt{5}-2-2\sqrt{5}\)
=-2
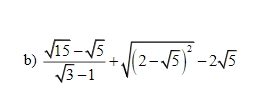
Bài 14:
\(A\left(x\right)+B\left(x\right)=5x^4-6x^3-3x^2-4\)
\(A\left(x\right)-B\left(x\right)=3x^4+7x^2+8x+2\)
Do đó: \(A\left(x\right)+B\left(x\right)+A\left(x\right)-B\left(x\right)=5x^4-6x^3-3x^2-4+3x^4+7x^2+8x+2\)
=>\(2\cdot A\left(x\right)=8x^4-6x^3+4x^2+8x-2\)
=>\(A\left(x\right)=4x^4-3x^3+2x^2+4x-1\)
Ta có: \(A\left(x\right)+B\left(x\right)=5x^4-6x^3-3x^2-4\)
=>\(B\left(x\right)=5x^4-6x^3-3x^2-4-4x^4+3x^3-2x^2-4x-1\)
=>\(B\left(x\right)=x^4-3x^3-5x^2-4x-5\)
Bài 13:
\(f\left(x\right)+g\left(x\right)=6x^4-3x^2-5\)
\(f\left(x\right)-g\left(x\right)=4x^4-6x^3+7x^2+8x-9\)
Do đó: \(f\left(x\right)+g\left(x\right)+f\left(x\right)-g\left(x\right)=6x^4-3x^2-5+4x^4-6x^3+7x^2+8x-9\)
=>\(2\cdot f\left(x\right)=10x^4-6x^3+4x^2+8x-14\)
=>\(f\left(x\right)=5x^4-3x^3+2x^2+4x-7\)
\(f\left(x\right)+g\left(x\right)=6x^4-3x^2-5\)
=>\(g\left(x\right)=6x^4-3x^2-5-5x^4+3x^3-2x^2-4x+7=x^4+3x^3-5x^2-4x+2\)