Question

[Anh Khôi Trần]

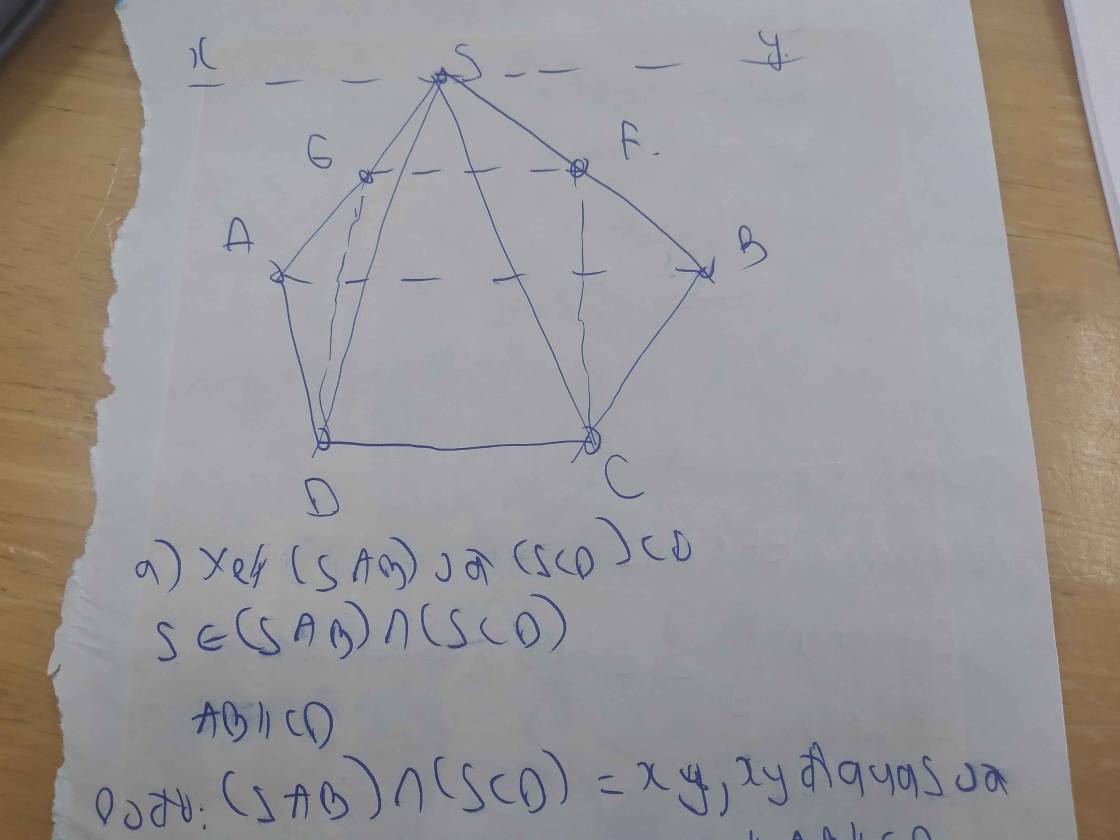
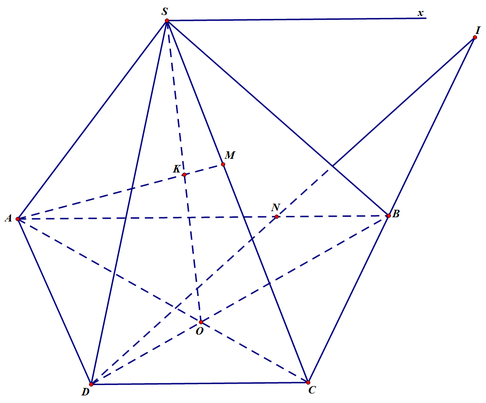
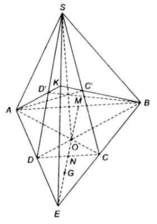
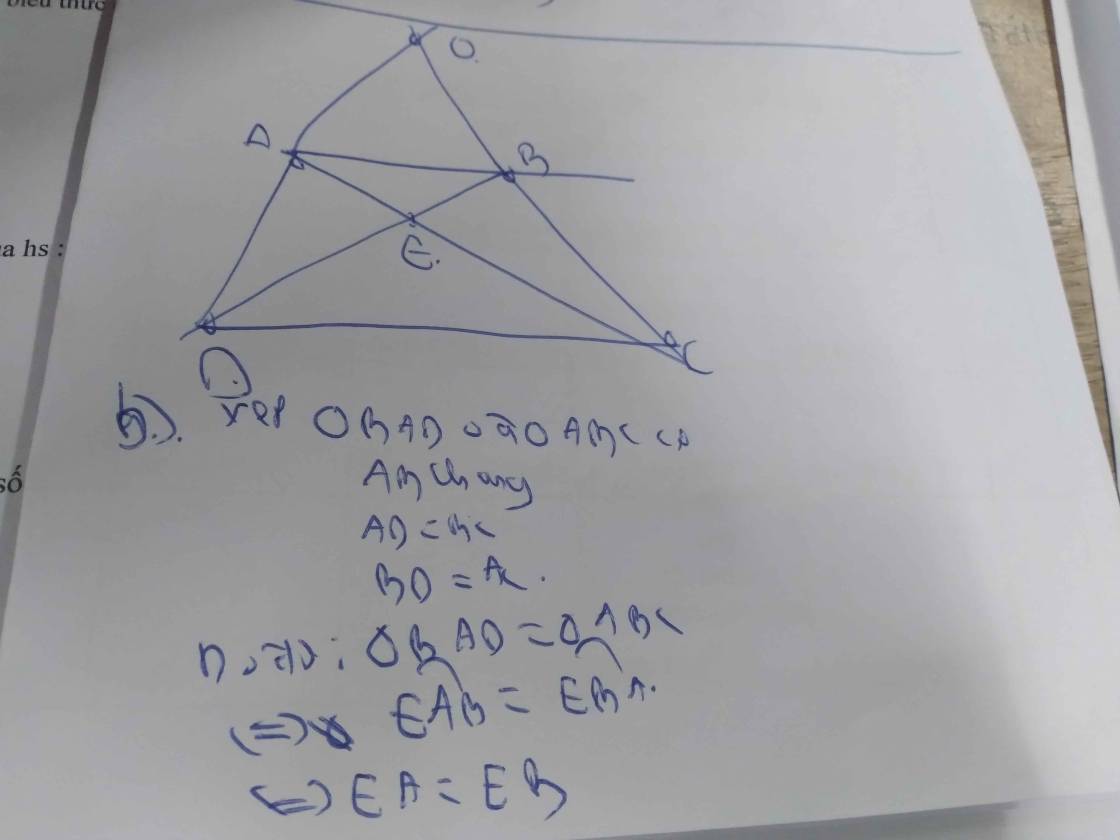
Bài 15: Cho hình thang \(A B C D\) (đáy lớn \(C D\)). Gọi \(O\) là giao điểm của \(A C\) và \(B D\); các đường kẻ từ \(A\) và \(B\) lần lượt song song với \(B C\) và \(A D\) cắt các đường chéo \(B D\) và \(A C\) tương ứng ở \(F\) và \(E\). Chứng minh:

\(E F \parallel A B .\)

Answer 1

[Dương Thu Nga]

Trả lời đc

Vì \(E F\) nối hai điểm \(E\) và \(F\), trong đó

• \(E\) là giao điểm của đường thẳng từ \(B\) song song với \(A D\) cắt \(A C\).
• \(F\) là giao điểm của đường thẳng từ \(A\) song song với \(B C\) cắt \(B D\).

1. Xét các tam giác có liên quan:

• Trong tam giác \(A B C\), đường thẳng \(A F\) song song với \(B C\) nên theo định lý Thales,

\(\frac{A B}{F C} = \frac{A F}{B C} \Rightarrow \text{t}ỉ\&\text{nbsp};\text{l}ệ\&\text{nbsp};\text{c} \overset{ˊ}{\text{a}} \text{c}\&\text{nbsp};đ\text{o}ạ\text{n}\&\text{nbsp};\text{th}ẳ\text{ng}\&\text{nbsp};\text{t}ưo\text{ng}\&\text{nbsp};ứ\text{ng}.\)

• Tương tự trong tam giác \(A B D\), đường thẳng \(B E\) song song với \(A D\) nên

\(\frac{A B}{E D} = \frac{B E}{A D} .\)

1. Do đó, các đoạn thẳng \(E F\) và \(A B\) có tỉ lệ tương ứng và nằm trong các tam giác có cạnh song song nên \(E F \parallel A B\).