K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 7 2021
a) Vì (d): y=ax+b//y=3x+1 nên \(\left\{{}\begin{matrix}a=3\\b\ne1\end{matrix}\right.\)
Suy ra: (d): y=3x+b
Thay x=2 và y=-2 vào (d), ta được:
\(3\cdot2+b=-2\)
\(\Leftrightarrow b=-8\)(thỏa ĐK)
Vậy: (d): y=3x-8
17 tháng 7 2021
b) Để (d) vuông góc với y=2x+3 nên \(2a=-1\)
hay \(a=-\dfrac{1}{2}\)
Vậy: (d): \(y=\dfrac{-1}{2}x+b\)
Thay x=-3 và y=4 vào (d), ta được:
\(\dfrac{-1}{2}\cdot\left(-3\right)+b=4\)
\(\Leftrightarrow b+\dfrac{3}{2}=4\)
hay \(b=\dfrac{5}{2}\)
Vậy: (d): \(y=\dfrac{-1}{2}x+\dfrac{5}{2}\)
25 tháng 6 2023
a: Thay x=0 và y=-5 vào (d), ta được:
2(m+1)*0-m^2-4=-5
=>m^2+4=5
=>m=1 hoặc m=-1
b:
PTHĐGĐ là;
x^2-2(m+1)x+m^2+4=0
Δ=(2m+2)^2-4(m^2+4)
=4m^2+8m+4-4m^2-16=8m-12
Để PT có hai nghiệm phân biệt thì 8m-12>0
=>m>3/2
x1+x2=2m+2; x1x2=m^2+4
(2x1-1)(x2^2-2m*x2+m^2+3)=21
=>(2x1-1)[x2^2-x2(2m+2-2)+m^2+4-1]=21
=>(2x1-1)[x2^2+2x2-x2(x1+x2)+x1x2-1]=21
=>(2x1-1)(x2^2+2x2-x1x2-x2^2+x1x2-1]=21
=>(2x1-1)(2x2-1)=21
=>4x1x2-2(x1+x2)+1=21
=>4(m^2+4)-2(2m+2)+1=21
=>4m^2+16-4m-4-20=0
=>4m^2-4m-8=0
=>(m-2)(m+1)=0
=>m=2(nhận) hoặc m=-1(loại)
2 tháng 3 2022
a, (d) đi qua I(1;3)
<=> 3 = 2(m-1) + m^2 + 2m
\(\Leftrightarrow m^2+4m-2=3\Leftrightarrow m^2+4m-5=0\)
\(\Leftrightarrow\left(m-1\right)\left(m+5\right)=0\Leftrightarrow m=1;m=-5\)
2 tháng 3 2022
a: Thay x=1 và y=3 vào (d),ta được:
2(m-1)+m2+2m=3
\(\Leftrightarrow m^2+4m-2-3=0\)
=>(m+5)(m-1)=0
=>m=-5 hoặc m=1
HP
17 tháng 12 2020
Đường thẳng (d) có dạng \(y=kx+m\)
\(A\left(0;2\right)\in\left(d\right)\Rightarrow m=2\)
\(\Rightarrow y=kx+2\left(d\right)\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm phân biệt khi phương trình \(x^2+\left(4-k\right)x+1=0\) có hai nghiệm phân biệt
\(\Leftrightarrow\Delta=\left(k-2\right)\left(k-6\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}k>6\\k< 2\end{matrix}\right.\)
Ta có \(x_1=\dfrac{k-4+\sqrt{k^2-8k+12}}{2}\Rightarrow y_1=\dfrac{k^2-4k+4+k\sqrt{k^2-8k+12}}{2}\)
\(\Rightarrow E\left(\dfrac{k-4+\sqrt{k^2-8k+12}}{2};\dfrac{k^2-4k+4+k\sqrt{k^2-8k+12}}{2}\right)\)
\(x_1=\dfrac{k-4-\sqrt{k^2-8k+12}}{2}\Rightarrow y_1=\dfrac{k^2-4k+4-k\sqrt{k^2-8k+12}}{2}\)
\(\Rightarrow F\left(\dfrac{k-4-\sqrt{k^2-8k+12}}{2};\dfrac{k^2-4k+4-k\sqrt{k^2-8k+12}}{2}\right)\)
Tọa độ trung điểm \(I\left(\dfrac{k-4}{2};\dfrac{k^2-4k+4}{2}\right)\)
\(x-2y+3=0\left(d'\right)\)
\(I\left(\dfrac{k-4}{2};\dfrac{k^2-4k+4}{2}\right)\in\left(d'\right)\Rightarrow\dfrac{k-4}{2}-\left(k^2-4k+4\right)+3=0\)
\(\Leftrightarrow2k^2-9k+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}k=\dfrac{9+\sqrt{33}}{2}\left(l\right)\\k=\dfrac{9-\sqrt{33}}{2}\left(tm\right)\end{matrix}\right.\)
\(\Leftrightarrow k=\dfrac{9-\sqrt{33}}{2}\)
P/s: Không biết đúng kh.
H
1 tháng 4 2021
Gọi đường thẳng (d) có hàm số y=kx+b (k khác 0) (do hàm số có hệ số góc là k )
Vì (d) đi qua I(0;-1) => -1=0k+b => b=-1
=> y=kx-1(d)
Xét phương trình hoành độ giao điểm chung của (P) và (d) ta có:
-x^2=kx-1
<=> x^2-kx-1=0 (1)
Xét phương trình có a=1;c=-1 => ac=-1 <0
=> (1) luôn có 2 nghiệm phân biệt
=> (P) và (d) luôn cắt nhau tại 2 điểm phân biệt
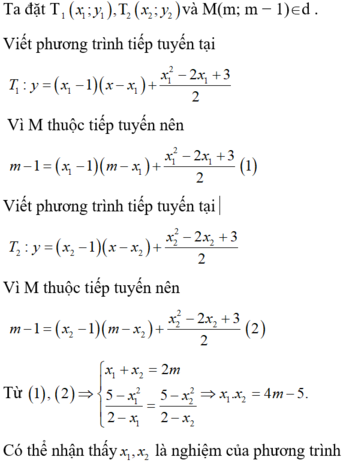
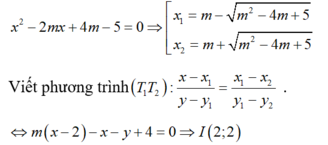
a: (P): \(y=-\frac{x^2}{4}\)
Bảng giá trị:
x
-4
-2
0
2
4
y
-4
-1
0
-1
-4
Vẽ đồ thị:
(D) có hệ số góc là m nên (D): y=mx+b
Thay x=3/2 và y=1 vào (D), ta được:
\(m\cdot\frac32+b=1\)
=>\(b=1-\frac32m\)
=>\(y=mx+1-\frac32m\)
b: Phương trình hoành độ giao điểm là:
\(-\frac14x^2=mx+1-\frac32m\)
=>\(-\frac14x^2-mx-1+\frac32m=0\)
Ta có: \(\Delta=\left(-m\right)^2-4\cdot\left(-\frac14\right)\left(-1+\frac32m\right)\)
\(=m^2+\left(-1+\frac32m\right)=m^2+\frac32m-1\)
Để (P) tiếp xúc với (D) thì Δ=0
=>\(m^2+\frac32m-1=0\)
=>\(2m^2+3m-2=0\)
=>\(2m^2+4m-m-2=0\)
=>(m+2)(2m-1)=0
=>\(\left[\begin{array}{l}m+2=0\\ 2m-1=0\end{array}\right.\Rightarrow\left[\begin{array}{l}m=-2\\ m=\frac12\end{array}\right.\)
c: Để (P) cắt (d) tại hai điểm phân biệt thì Δ>0
=>\(m^2+\frac32m-1>0\)
=>\(2m^2+3m-2>0\)
=>(m+2)(2m-1)>0
=>\(\left[\begin{array}{l}m>\frac12\\ m<-2\end{array}\right.\)
Cho parabol P: y = -x²/4 và đường thẳng d đi qua điểm I(3/2; 1), có hệ số góc là m
a) Viết phương trình D và vẽ P
Vì d đi qua điểm I(3/2;1) và có hệ số góc m nên phương trình d có dạng:
y = m(x - 3/2) + 1
⇒ y = mx - 3m/2 + 1
Vậy phương trình d: y = mx - 3m/2 + 1
Đồ thị P là một parabol có đỉnh tại gốc tọa độ, bề lõm hướng xuống. Một số điểm đặc trưng:
x = 0 ⇒ y = 0
x = 2 ⇒ y = -1
x = -2 ⇒ y = -1
x = 4 ⇒ y = -4
x = -4 ⇒ y = -4
Nối các điểm lại ta được đồ thị parabol P
b) Tìm m để d tiếp xúc P
Xét phương trình hoành độ giao điểm giữa d và P:
mx - 3m/2 + 1 = -x²/4
⇔ x²/4 + mx - 3m/2 + 1 = 0
Đây là phương trình bậc hai theo x. Để tiếp xúc thì phương trình phải có nghiệm kép
Điều kiện để tiếp xúc: phương trình có Δ = 0
Δ = m² - 4·(1/4)·(-3m/2 + 1)
= m² - (-3m/2 + 1)
= m² + 3m/2 - 1
Cho Δ = 0:
m² + 3m/2 - 1 = 0
Nhân cả hai vế với 2:
2m² + 3m - 2 = 0
Giải phương trình:
Δ = 9 + 16 = 25
⇒ m = [-3 ± √25]/4
⇒ m = (-3 + 5)/4 = 1/2
hoặc m = (-3 - 5)/4 = -2
Vậy d tiếp xúc với P khi m = 1/2 hoặc m = -2
c) Tìm m để d và P có hai điểm chung phân biệt
Khi d và P cắt nhau tại 2 điểm phân biệt thì phương trình hoành độ giao điểm phải có hai nghiệm phân biệt
Tức là Δ > 0
Ta có:
Δ = m² + 3m/2 - 1
Δ > 0 ⇒ m² + 3m/2 - 1 > 0
⇔ 2m² + 3m - 2 > 0
Giải bất phương trình:
2m² + 3m - 2 > 0
Nghiệm của phương trình là m = 1/2 và m = -2
Bất phương trình đúng khi:
m < -2 hoặc m > 1/2
Vậy d và P có hai điểm chung phân biệt khi m < -2 hoặc m > 1/2
Cho mình xin 1 tick với ạ.