Tất cả các nghiệm không tầm thường của hàm zeta Riemann (ζ(s)) đều có phần thực bằng 21.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 8
q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)q(≧▽≦q)
CM
24 tháng 10 2019
Ta có 
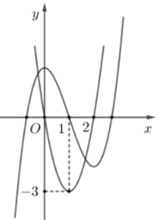
Quan sát đồ thị có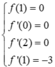 
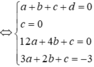
Đặt 
phương trình trở thành:
Khi đó 
Phương trình này có 3 nghiệm phân biệt
Tổng các phần tử củaS bằng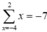 
Chọn đáp án C.
CM
24 tháng 11 2018
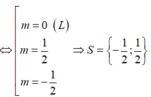
Vậy tổng các giá trị tuyệt đối của tất cả các phần tử thuộc S là 1.
Chọn C
CM
16 tháng 3 2019
Đáp án B.
Pt tiếp tuyến đi qua A có dạng y=k(x-a)+1
Để có đúng 1 tiếp tuyến đi qua A thì hpt
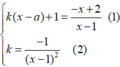
có đúng một nghiệm
Thay (2) vào (1):
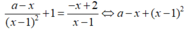
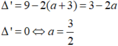
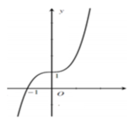
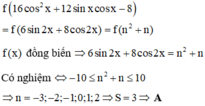
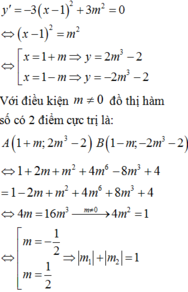
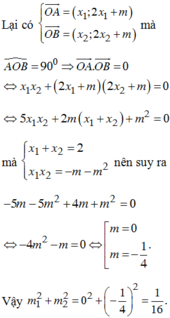
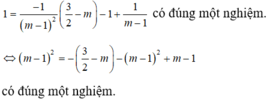
anh/em/bạn nên để cho đúng lớp nhé.
Bạn có thể thấy, chỉ với một câu nói ngắn gọn như vậy, nhưng nó đã làm đau đầu biết bao thế hệ nhà toán học vĩ đại.
Đây thực sự là một thách thức cực lớn! Bạn có muốn mình giải thích thêm về hàm zeta Riemann hay các khái niệm liên quan như nghiệm không tầm thường và phần thực để bạn có cái nhìn rõ hơn không?