\(a=73a+27a+100b\) với\(a+b=41\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
4
SM
7 tháng 7 2018
M = 73a + 27a + 100b
M = ( 73 + 27 )a + 100b
M = 100a + 100b
M = 100.(a + b)
mà a + b = 41
=>M = 100 . 41 = 4100
Chúc bạn học giỏi!!!
NV
1
NV
0
CM
17 tháng 11 2019
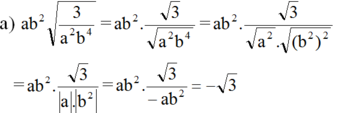
(vì a < 0 nên |a| = -a, b2 > 0 với mọi b ≠ 0 nên |b2| = b2 )
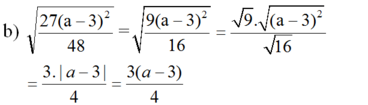
(vì a > 3 nên |a - 3| = a - 3)
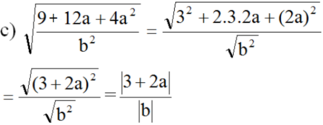
Vì b < 0 nên |b| = -b
Vì a ≥ -1,5 nên 3 + 2a ≥ 0. Do đó: |3 + 2a| = 3 + 2a
Vậy:
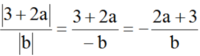
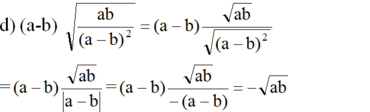
(vì a < b < 0 và b < 0 nên |a - b| = -(a - b), ab > 0)
K
1
2 tháng 2 2019
(18a-5b).(27a+b) chia hết cho 17
Mà 17 là số nguyên tố nên trong 2 số 18a-5b và 27a+b có ít nhất 1 số chia hết cho 17
Xét hiệu: 5.(27a+b)+(18a-5b)
= 135a+5b+18a-5b
= 153a chia hết cho 17 (*)
+ Nếu 27a+b chia hết cho 17 từ (*) dễ dàng => 18a-5b chia hết cho 17
=> (27a+b)(18a-5b) chia hết cho 17.17 = 289
+ Nếu 18a-5b chia hết cho 17, từ (*) => 5.(27a+b) chia hết cho 17
Mà (5;17)=1 nên 27a+b chia hết cho 17
Do đó, (18a-5b)(27a+b) chia hết cho 17.17 = 289
Vậy ta có đpcm
Học tốt
9 tháng 10 2021
\(a,=6\left|a\right|b^2\sqrt{2}=6ab^2\sqrt{2}\\ b,=3\left|ab\right|\sqrt{3a}=-3ab\sqrt{3a}\)
D
1
AH
Akai Haruma
Giáo viên
30 tháng 11 2021
Lời giải:
$a+b=0,16$
$\Leftrightarrow 100(a+b)=100.0,16$
$\Leftrightarrow 100a+100b=16$
Vậy pt (1) và (2) tương đương, nên hpt có nghiệm: $(a,b)=(m, 16-m)$ với $m$ là số thực bất kỳ.
NT
1
PA
2
3 tháng 10 2021
a: \(A=10^{30}=1000^{10}\)
\(B=2^{100}=1024^{10}\)
mà 1000<1024
nên A<B
b: \(A=3^{450}=27^{150}\)
\(B=5^{300}=25^{150}\)
mà 27>25
nên A>B
VM
0
a=4100, b=−4059
a=73a+27a+100b
=100a+100b
=100(a+b)
\(=100\cdot41=4100\)