viết tập hợp F các số tự nhiên x mà \(x\) \(\notin\) \(N^{\cdot}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DM
8
LV
16 tháng 8 2016
Vì x không thuộc N* và là số thự nhiên
=> Ta có:
A = {x thuộc N | x không thuộc N*}
A = {0}
ỦNG HỘ NHA
HW
3
23 tháng 8 2016
A = { 1; 2 ; 3 ; 4; ... }
Tập hợp A không dừng lại ở số nào.
A = { 1; 2 ; 3 ; 4; ... }
Tập hợp A không dừng lại ở số nào.
A = { 1; 2 ; 3 ; 4; ... }
Tập hợp A không dừng lại ở số nào.
A = { 1; 2 ; 3 ; 4; ... }
Tập hợp A không dừng lại ở số nào.
Hari Won Tích nha
LD
4
NN
1
18 tháng 8 2015
x \(\notin\)N* => x \(\ne\){1;2;3;4;....}
=> x = 0
Vậy A = {0}
CM
7 tháng 4 2019
a. A = {8}. Vậy tập hợp A có 1 phần tử.
b. B = {0;1;2;…}. Vậy tập hợp B có vô số phần tử.
c. C = {5}. Vậy tập hợp C có 1 phần tử.
d. D = ∅ . Vậy tập hợp D không có phần tử nào.
e. E = {0;1;2;…}. Vậy tập hợp E có vô số phần tử.
f. F = ∅ . Vậy tập hợp F không có phần tử nào.
g. G = {0;1;2;3}. Vậy tập hợp G có 4 phần tử
CM
28 tháng 11 2019
a, x – 9 = 13 => x = 13 + 9 => x = 22
Vậy M = {22} và M có 1 phần tử
b, x + 6 = 34
x = 34 – 6
x = 28
Vậy H = {28} và H có 1 phần tử.
c, x.0 = 0 luôn đúng với mọi x ∈ N
Vậy O = N và O có vô số phần tử
d, a) x.0 = 3 không thỏa mãn vì trong tập hợp các số tự nhiên, số nào nhân với 0 cũng bằng 0
Vậy A = { ∅ } và A có 0 phần tử
e, (x – 2)(x – 5) = 0
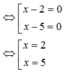
Vậy N = {2;5} và N có 2 phần tử
f, a) x : 0 = 0 không có số tự nhiên nào thỏa mãn vì không thể chia cho 0
Vậy G = { ∅ } và G có 0 phần tử
25 tháng 8 2016
1. \(x\in\left\{0\right\}\)
2. Gọi x là số cần tìm => x = n - 1
F = ∅
\(x\notin N^{\star}\)
mà x là số tự nhiên
nên x=0
=>F={0}