Giải phương trình:
a)\(3x+1-√(3x^2+7)-√(3x-1)=0\)
b)\(^3√(x^2-1)+x=√(x^3-1)\)
c)\(x(x+1)(x-3)+3=√(4-x)+√(1+x)\)
SOS!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

phương trình tích là phương trình có dạng A*B=0
=>A=0 hoặc B=0

x 3 – 8 = 0
⇔ (x − 2)( x 2 + 2x + 4) = 0
⇔ x 1 = 2; x 2 = −1 + i 3 ; x 2 = −1 - i 3

x 3 + 8 = 0
⇔ (x + 2)( x 2 − 2x + 4) = 0
⇔ x 1 = −2; x 2 = 1 + i 3 ; x 3 = 1 - i 3

z 2 – 2z + 13 = 0
có Δ' = 1 - 13 = 12 < 0
⇒ Phương trình có hai nghiệm phân biệt: 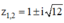
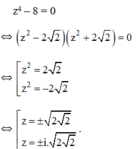
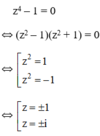
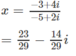
c) đkxđ: \(-1\le x\le4\)
pt đã cho tương đương với:
\(x\left(x+1\right)\left(x-3\right)=\left\lbrack\sqrt{4-x}+\left(\frac13x-2\right)\right\rbrack+\left\lbrack\sqrt{1+x}-\left(\frac13x+1\right)\right\rbrack\)
\(\lrArr x\left(x+1\right)\left(x-3\right)=\frac{4-x-\left(\frac13x-2\right)^2}{\sqrt{4-x}-\left(\frac13x-2\right)}+\frac{1+x-\left(\frac13x+1\right)^2}{\sqrt{1+x}-\left(\frac13x+1\right)}\)
\(\lrArr x\left(x+1\right)\left(x-3\right)=\frac{-\frac19x^2+\frac13x}{\sqrt{4-x}-\frac13x+2}+\frac{-\frac19x^2+\frac13x}{\sqrt{1+x}+\frac13x+1}\)
\(\lrArr x\left(x+1\right)\left(x-3\right)=\frac{-\frac19x\left(x-3\right)}{\sqrt{4-x}-\frac13x+2}+\frac{-\frac19x\left(x-3\right)}{\sqrt{1+x}+\frac13x+1}\)
\(\lrArr\left[\begin{array}{l}x\left(x-3\right)=0\left(1\right)\\ x+1=\frac{-1}{9\left(\sqrt{4-x}-\frac13x+2\right)}+\frac{-1}{9\left(\sqrt{1+x}+\frac13x+1\right)}\left(2\right)\end{array}\right.\)
(1) \(\lrArr\left[\begin{array}{l}x=0\\ x=3\end{array}\right.\) (nhận)
(2) vô nghiệm vì VT>0 trong khi VP<0.
Vậy tập nghiệm của pt đã cho là \(S=\left\lbrace0;3\right\rbrace\)