cho em xin cách giải bài này với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

#include <bits/stdc++.h>
using namespace std;
int main (){
int n;
cin >> n;
int a[n];
long long t=0,k=0;
for (int i=1;i<=n;i++) cin >> a[i];
for (int i=1;i<=n;i++) {
int lt=1;
for (int j=1;j<=i;j++)
lt=lt*a[i];
t=t+lt;
}
cout << t;
return 0;
}

a) x - 15 x 7 - 270 : 45 = 169
x- 105 - 6 = 169
x = 169 + 6 + 150
x = 325
b)[(4x + 28 ) x 3 + 55 ] : 5 = 35
[12x + 84 + 55 ] = 35 x 5
12x + 139 = 175
12x = 175 - 139
12x = 36
x = 36 : 12
x = 3
c)(455 - x : 2 x 6) : 5 = 31
455 - x : 2 x 6 = 31 x 5
455 - x : 2 x6 = 155
x : 2 x 6 = 455 - 155
x : 2 x6 = 300
x : 2 = 300 : 6
x: 2 = 50
x = 50 x 2
x= 100

3 ) Ngày thứ nhất cửa bán được
42 x \(\dfrac{2}{7}=12\) (bao đường)
Ngày thứ hai cửa hàng bán được
(42 - 12) x \(\dfrac{3}{5}\) = 18 (bao đường)
Cửa hàng còn lại số bao đường
42 - 12 - 18 = 12 (bao đường)
Đáp số 12 bao đường
Tỉ số cam và xoài là
\(\dfrac{1}{2}:\dfrac{2}{5}=\dfrac{5}{4}\)
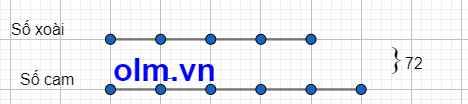
Số cam là
72: ( 5+4) x 5 = 40 (cam)
Số xoài là
72 - 40 = 32 (xoài)
Đáp số : xoài 32 quả
cam 40 quả


10:
\(a+b=50^0+40^0=90^0\)
=>\(sina=cosb;sinb=cosa;tana=cotb;cota=tanb\)
=>sina=cosb
=>Chọn C
11:
Xét ΔABC vuông tại A có \(AC=BC\cdot sinB\)
=>\(AC=12\cdot sin30=6\)
=>Chọn B

có thể viết được : 4670,4760,6740,6470,7460,7640,4706,4607,6704,

Hệ thức lượng tam giác MAO: \(MA^2=MH.MO\)
\(\Rightarrow MH.MO=MB.MC\Rightarrow\dfrac{MH}{MC}=\dfrac{MC}{MO}\)
\(\widehat{OMB}\) chung
\(\Rightarrow\Delta MCH\sim\Delta MOB\)
\(\Rightarrow\widehat{B}=\widehat{MHC}\)
Mà \(\widehat{B}=\widehat{ADC}\) (cùng chắn AC) \(\Rightarrow\widehat{MHC}=\widehat{ADC}\)
\(\widehat{MHC}+\widehat{CHD}=\widehat{MHD}=90^0\Rightarrow\widehat{ADC}+\widehat{CHD}=90^0\)
\(\Rightarrow\widehat{HCD}=90^0\) (đpcm)
Điểm K cho nhằm mục đích làm rối tinh thần :D
Để giải bài tập này, trước tiên ta cần xác định diện tích sử dụng cho ghế và bàn, cũng như diện tích mặt sàn dành cho lưu thông.
a) Diện tích tổng cộng của gian hàng là $$60m^{2}$$60m2. Diện tích để kê một chiếc ghế là $$0,5m^{2}$$0,5m2 và một chiếc bàn là $$1,2m^{2}$$1,2m2. Diện tích dành cho lưu thông tối thiểu là $$12m^{2}$$12m2. Do đó, diện tích còn lại để kê ghế và bàn sẽ là $$60m^{2} - 12m^{2} = 48m^{2}$$60m2−12m2=48m2
Ta có thể viết bất phương trình như sau:
$$0,5x + 1,2y \leq 48$$0,5x+1,2y≤48
b) Để tìm ba nghiệm của bất phương trình trên, ta có thể chọn các giá trị cho x và y thỏa mãn bất phương trình.
Tóm lại, ba nghiệm của bất phương trình là: $$(0, 40)$$(0,40), $$(96, 0)$$(96,0), và $$(24, 30)$$(24,30)
a: Diện tích phần dành cho mặt sàn để kê bàn và ghế tối đa là:
\(60-12=48\left(m^2\right)\)
Diện tích để kê x chiếc ghế là \(0,5x\left(m^2\right)\)
Diện tích để kê y chiếc bàn là \(1,2y\left(m^2\right)\)
Diện tích phần dành cho mặt sàn để kê bàn và ghế tối đa là \(48m^2\) nên ta có:
0,5x+1,2y<=48
b: 0,5x+1,2y<=48
=>5x+12y<=480
Khi x=0 và y=0 thì \(5x+12y=5\cdot0+12\cdot0=0\le480\) (đúng)
Khi x=0;y=30 thì \(5x+12y=5\cdot0+12\cdot30=360\le480\) (đúng)
Khi x=1;y=3 thì \(5x+12y=5\cdot1+12\cdot3=5+36=41\le480\) (đúng)
vậy: 3 nghiệm của bất phương trình là (0;0); (0;30); (1;3)