K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
B
1
12 tháng 9 2021
Ta có: \(\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}+\sqrt{\left(2-\sqrt{5}\right)^2}-2\sqrt{5}\)
\(=\sqrt{5}+\sqrt{5}-2-2\sqrt{5}\)
=-2
AH
Akai Haruma
Giáo viên
30 tháng 9 2024
Lời giải:
a. $(x^3+x^2y+xy^2+y^3)(x-y)=[x^2(x+y)+y^2(x+y)](x-y)$
$=(x^2+y^2)(x+y)(x-y)=(x^2+y^2)(x^2-y^2)=x^4-y^4$
b.
$(2x-1)(x+3)=2x(x+3)-(x+3)=2x^2+6x-x-3=2x^2+5x-3$
NL
2
26 tháng 1 2021
\(\frac{1515}{2525}=\frac{15x101}{25x101}=\frac{3}{5}\)
TT
26 tháng 10 2020
Nếu nhớ không nhầm thì hướng dẫn chi tiết cho rồi :vv
\(x^7+x^2+1=x\left(x^6-1\right)+\left(x^2+x+1\right)\)
\(=x\left(x^3-1\right)\left(x^3+1\right)+\left(x^2+x+1\right)\)
\(=x\left(x-1\right)\left(x+1\right)\left(x^2-x+1\right)\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left[\left(x^3-x\right)\left(x^2-x+1\right)+1\right]\)
P/s : ko chắc lém :)))
30 tháng 10 2017
60 = 5 . 3 . 22
280 = 5 . 7 . 23
=> ƯCLN ( 60 ; 280 ) = 5 . 22 = 20
KV
15 tháng 11 2023
Số tuổi mẹ tăng thêm kể từ khi sinh con:
42 - 27 = 15 (năm)
Số tuổi của con bằng số tuổi mẹ tăng thêm nên con 15 tuổi
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 11 2023
Kiến thức quan trọng cần nhớ với các bài toán về tuổi là hiệu số tuổi luôn không đổi theo thời gian em nhé
Giải
Vì mỗi năm mỗi người tăng thêm một tuổi nên hiệu số tuổi của hai mẹ con luôn không đổi theo thời gian.
Mẹ sinh con năm mẹ 27 tuổi vậy mẹ hơn con 27 tuổi, hiện nay mẹ vẫn hơn con 27 tuổi.
Từ những lập luận trên ta có:
Tuổi con hiện nay là: 42 - 27 = 15 (tuổi)
Đáp số: 15 tuổi.
TT
20 tháng 10 2020
Phương pháp :
+) Ta nhẩm các ước nguyên của hệ số tự do
+) Trong trường hợp ước nguyên của hệ số tự do không là nghiệm của đa thức, ta thử vs các số là (ước của hệ số tự do)/(ước của hệ số bậc cao nhất của đa thức) <Lưu ý nên thử từ bé đến lớn :)))
Trong trường hợp thử 2 trường hợp trên không đc thì dùng hệ số bất định!!! (Có lần ra nghiệm nguyên :v nhưng bấm sai => mình dùng hệ số bất định, nháp 3 trang làm vào 3 dòng :vv)
11 tháng 2 2022
\(A=\dfrac{-1}{5}x^3\cdot\dfrac{1}{32}x^{20}y^5\cdot\dfrac{64}{27}x^3y^9\cdot z^{2022}=-\dfrac{2}{135}x^{26}y^{14}z^{2022}\)
11 tháng 2 2022
`A=\frac{-1}{5}x^3 \times \frac{1}{32}x^{20}y^5 \times \frac{64}{27}x^3y^9 \times z^{2022}=-\frac{2}{135}x^{26}y^{14}z^{2022}`
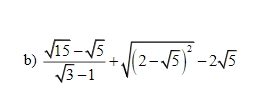
a: \(\left(2x-1\right)^2-x\left(4x-3\right)\)
\(=4x^2-4x+1-4x^2+3x\)
=-x+1
b: \(\left(x-2\right)\left(x-1\right)-\left(x-3\right)^2\)
\(=x^2-3x+2-\left(x^2-6x+9\right)\)
\(=x^2-3x+2-x^2+6x-9=3x-7\)
c: \(\left(x-2\right)^3-x\left(x-1\right)\left(x-2\right)\)
\(=x^3-6x^2+12x-8-x\left(x^2-3x+2\right)\)
\(=x^3-6x^2+12x-8-x^3+3x^2-2x\)
\(=-3x^2+10x-8\)
d: \(\frac12x\left(x-2\right)-\left(2x-3\right)^2\)
\(=\frac12x^2-x-\left(4x^2-12x+9\right)\)
\(=\frac12x^2-x-4x^2+12x-9=-\frac72x^2+11x-9\)