(a+a)x4:8=a
hỏi a là bao nhiêu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 11 2019
Đặt t = x 2 ≥ 0
Phương trình (1) thành t 2 + 2 t + a = 0 2
Phương trình (1) có đúng 4 nghiệm
⇔ phương trình (2) có 2 nghiệm dương phân biệt
⇔ Δ > 0 S > 0 P > 0 ⇔ 4 − 4 a > 0 − 2 > 0 a > 0 ( v l ) ⇔ a ∉ ∅
Đáp án cần chọn là: A
CM
22 tháng 4 2017
Đặt t = x 2 ≥ 0
Phương trình (1) thành t 2 + 2 t + a = 0 1
Phương trình (1) có đúng 3 nghiệm phân biệt
=> phương trình (2) có một nghiệm bằng 0 và nghiệm còn lại dương.
(2) có nghiệm t = 0 ⇔ 0 2 + 2 . 0 + a = 0 ⇔ a = 0
Khi đó phương trình trở thành t 2 + 2 t = 0 ⇔ t = 0 t = − 2 < 0 nên không thỏa mãn yêu cầu bài toán.
Vậy không có giá trị nào của a thỏa mãn bài toán.
Đáp án cần chọn là: A
CM
3 tháng 11 2018
Đáp án A
Xét g x = x 4 − 4 x 3 + 4 x 2 + a
g ' x = 4 x 3 − 12 x 2 + 8 x = 0 ⇔ x = 0 , 1 , 2
CM
5 tháng 6 2019
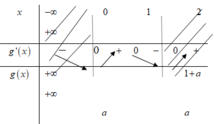
+ Xét hàm số y= x4- 4x3+ 4x2+ a trên đoạn [ 0; 2].
Ta có đạo hàm y’ = 4x3-12x2+ 8x,
y
'
=
0
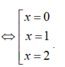
Khi đó; y( 0) = y( 2) = a; y( 1) = a+ 1
+ Nếu a≥ 0 thì M= a+ 1,m = a.
Để M ≤ 2m khi a≥ 1, suy ra a ∈ 1 ; 2 ; 3 thỏa mãn
+ Nếu a≤ - 1 thì M = a = - a , m = a + 1 = - a - 1 .
Để M≤ 2m thì a≤ -2, suy ra a a ∈ - 2 ; - 3
Vậy có 5 giá trị nguyên của a thỏa mãn yêu cầu.
Chọn B.
CM
1 tháng 10 2018
Chọn D
Xét hàm số f(x) = x 4 - 4 x 3 + 4 x 2 + a trên đoạn [0;2], ta có:
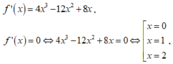
trên đoạn
Vì 
nên trên đoạn [0;2] giá trị lớn nhất và giá trị nhỏ nhất của hàm số 
lần lượt là a+1, a
Suy ra 
nếu 
nếu 
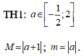
Khi đó 
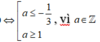
nên chọn 
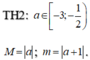
Khi đó 
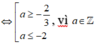nên chọn 
Vậy có 4 giá trị a thỏa yêu cầu
PT
Qua điểm A( 0;2 ) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị của hàm số y= x4-2x2+2
1
CM
23 tháng 6 2018
Gọi d là tiếp tuyến của đồ thị hàm số đã cho.
Vì A ∈ d nên phương trình của d có dạng: y= kx+2
Vì d tiếp xúc với đồ thị (C) nên hệ
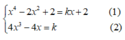
có nghiệm
Thay (2) vào (1) ta suy ra được
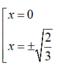
Chứng tỏ từ A có thể kẻ được 3 tiếp tuyến đến đồ thị (C)
Chọn B.
(a + a) x 4 : 8 = a
[ a x 1 + a x 1] x 4 : 8 = a
a x (1+ 1) x 4 : 8 = a
a x 2 x 4 : 8 = a
a x (2 x 4 : 8) = a
a x (8 : 8) = a
a x 1 = a
Vậy a là mọi số khác 0