K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
B
1
12 tháng 9 2021
Ta có: \(\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}+\sqrt{\left(2-\sqrt{5}\right)^2}-2\sqrt{5}\)
\(=\sqrt{5}+\sqrt{5}-2-2\sqrt{5}\)
=-2
10 tháng 11 2021
\(a,ĐK:x\ne\pm1;x\ne0\\ M=\dfrac{1-x+2x}{\left(1+x\right)\left(1-x\right)}:\dfrac{1-x}{x}\\ M=\dfrac{x+1}{\left(x+1\right)\left(1-x\right)}\cdot\dfrac{x}{1-x}=\dfrac{x}{\left(1-x\right)^2}\\ b,ĐK:x\ge0;x\ne4\\ N=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ N=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
Tất cả đều phải tìm điều kiện
DV
4
10 tháng 11 2021
Thằng kia hỏi ngu đến thế là cùng. Học lớp mấy rồi mà còn hỏi câu này.
8 tháng 9 2021
\(e,\left(5+2\sqrt{6}\right)\left(49-20\sqrt{6}\right)\sqrt{5-2\sqrt{6}}\\ =\left(5+2\sqrt{6}\right)\left(\sqrt{3}-\sqrt{2}\right)\left(5-2\sqrt{6}\right)^2\\ =\left(5-2\sqrt{6}\right)\left(\sqrt{3}-\sqrt{2}\right)\\ =\left(\sqrt{3}-\sqrt{2}\right)^2\left(\sqrt{3}-\sqrt{2}\right)=\left(\sqrt{3}-\sqrt{2}\right)^3\)
\(f,\left(2\sqrt{6}-4\sqrt{3}+5\sqrt{2}-\dfrac{1}{4}\sqrt{8}\right)\cdot3\sqrt{6}\\ =36-36\sqrt{2}+30\sqrt{3}-3\sqrt{3}=36-36\sqrt{2}+27\sqrt{3}\)
\(g,\left(2+\sqrt{3}-\sqrt{2}\right)\left(2-\sqrt{3}-\sqrt{2}\right)\left(3+\sqrt{2}\right)\sqrt{3-2\sqrt{2}}\\ =\left[\left(2-\sqrt{2}\right)^2-\left(\sqrt{3}\right)^2\right]\left(3+\sqrt{2}\right)\sqrt{\left(\sqrt{2}-1\right)^2}\\ =\left(3-4\sqrt{2}\right)\left(3+\sqrt{2}\right)\left(\sqrt{2}-1\right)\\ =\left(1-9\sqrt{2}\right)\left(\sqrt{2}-1\right)\\ =10\sqrt{2}-37\)
\(h,A=\sqrt{4+\sqrt{10+2\sqrt{5}}}+\sqrt{4-\sqrt{10+2\sqrt{5}}}\\ A^2=4+\sqrt{10+2\sqrt{5}}+4-\sqrt{10+2\sqrt{5}}+2\sqrt{\left(4+\sqrt{10+2\sqrt{5}}\right)\left(4-\sqrt{10+2\sqrt{5}}\right)}\\ A^2=8+2\sqrt{6-2\sqrt{5}}\\ A^2=8+2\left(\sqrt{5}-1\right)\\ A^2=6+2\sqrt{5}\\ A=\sqrt{6+2\sqrt{5}}=\sqrt{\left(\sqrt{5}+1\right)^2}=\sqrt{5}+1\)
8 tháng 9 2021
\(b,\sqrt{15-\sqrt{216}}+\sqrt{33-12\sqrt{6}}\\ =\sqrt{15-6\sqrt{6}}+\sqrt{\left(2\sqrt{6}-3\right)^2}\\ =\sqrt{\left(3-\sqrt{6}\right)^2}+2\sqrt{6}-3\\ =3-\sqrt{6}+2\sqrt{6}-3=\sqrt{6}\)
\(c,\sqrt{2-\sqrt{3}}\left(\sqrt{6}+\sqrt{2}\right)\\ =\sqrt{12-6\sqrt{3}}+\sqrt{4-2\sqrt{3}}\\ =\sqrt{\left(3-\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{3}-1\right)^2}\\ =3-\sqrt{3}+\sqrt{3}-1=2\)
8 tháng 9 2021
c: \(\sqrt{2-\sqrt{3}}\cdot\left(\sqrt{6}+\sqrt{2}\right)\)
\(=\sqrt{4-2\sqrt{3}}\cdot\left(\sqrt{3}+1\right)\)
\(=\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)\)
=3-1
=2
NL
2
NN
Nguyễn Ngọc Anh Minh
CTVHS
26 tháng 1 2021
\(\frac{1515}{2525}=\frac{15x101}{25x101}=\frac{3}{5}\)
10 tháng 11 2021
Tham khảo:
Điều kiện xác định của phương trình là tập hợp các giá trị của ẩn làm cho tất cả các mẫu trong phương trình đều khác 0. Điều kiện xác định của phương trình viết tắt là ĐKXĐ.
0H
1
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 3 2022
ĐKXĐ: \(x>2\)
\(A=\dfrac{\sqrt{x-2-4\sqrt{x-2}+4}+\sqrt{x-2+4\sqrt{x-2}+4}}{\sqrt{\left(\dfrac{2}{x}-1\right)^2}}\)
\(=\dfrac{\sqrt{\left(\sqrt{x-2}-2\right)^2}+\sqrt{\left(\sqrt{x-2}+2\right)^2}}{\left|\dfrac{2}{x}-1\right|}=\dfrac{\left|\sqrt{x-2}-2\right|+\left|\sqrt{x+2}+2\right|}{1-\dfrac{2}{x}}\)
- Với \(x\ge6\Rightarrow A=\dfrac{\sqrt{x-2}-2+\sqrt{x-2}+2}{\dfrac{x-2}{x}}=\dfrac{2x\sqrt{x-2}}{x-2}=\dfrac{2x}{\sqrt{x-2}}\)
- Với \(2< x< 6\Rightarrow A=\dfrac{2-\sqrt{x-2}+\sqrt{x-2}+2}{\dfrac{x-2}{x}}=\dfrac{4x}{x-2}\)
26 tháng 10 2021
Cho mk hỏi muốn rút gọn biểu thức có chứa căn bậc 4 thì làm thế nào nhỉ
Chỉ có cách là bạn phải phân tích số trong biểu thức ra làm căn bậc hai sau đó giải quyết căn 4 thành căn 2
Tùy vào đề bài sẽ có cách làm nha
HT
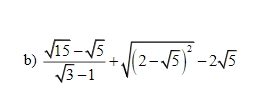
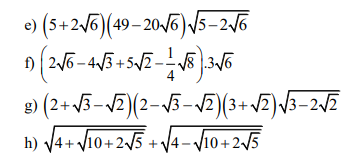
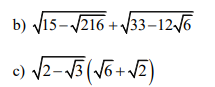
4: Sửa đề: \(x=\sqrt[3]{3+2\sqrt2}-\sqrt[3]{3-2\sqrt2}\)
=>\(x^3=3+2\sqrt2-\left(3-2\sqrt2\right)+3\cdot x\cdot\sqrt[3]{\left(3+2\sqrt2\right)\left(3-2\sqrt2\right)}\)
=>\(x^3=6+3\cdot x\cdot1=3x+6\)
\(y=\sqrt[3]{17+12\sqrt2}-\sqrt[3]{17-12\sqrt2}\)
=>\(y^3=17+12\sqrt2-\left(17-12\sqrt2\right)-3\cdot y\cdot\sqrt[3]{\left(17+12\sqrt2\right)\left(17-12\sqrt2\right)}\)
=>\(y^3=34-3y\)
\(H=\left(x-y\right)^3+3\left(x-y\right)\left(xy+1\right)\)
\(=\left(x-y\right)\left(x^2-2xy+y^2+3xy+3\right)=\left(x-y\right)\left(x^2+xy+y^2+3\right)\)
\(=\left(x^3-y^3\right)+3\left(x-y\right)\)
=(3x+6-34+3y)+3x-3y
=3x+3y+3x-3y-28
=6x-28
Bài 3:
a: \(A=\sqrt{13+30\cdot\sqrt{2+\sqrt{9+4\sqrt2}}}\)
\(=\sqrt{13+30\cdot\sqrt{2+\sqrt{8+2\cdot2\sqrt2\cdot1+1}}}\)
\(=\sqrt{13+30\cdot\sqrt{2+\sqrt{\left(2\sqrt2+1\right)^2}}}\)
\(=\sqrt{13+30\cdot\sqrt{2+\left(2\sqrt2+1\right)}}\)
\(=\sqrt{13+30\cdot\sqrt{2+2\sqrt2+1}}\)
\(=\sqrt{13+30\cdot\sqrt{\left(\sqrt2+1\right)^2}}\)
\(=\sqrt{13+30\cdot\left(\sqrt2+1\right)}=\sqrt{43+30\sqrt2}\)
\(=\sqrt{25+2\cdot5\cdot3\sqrt2+18}=\sqrt{\left(5+3\sqrt2\right)^2}=5+3\sqrt2\)
b: \(B=\frac{3+\sqrt5}{2\sqrt2+\sqrt{3+\sqrt5}}+\frac{3-\sqrt5}{2\sqrt2-\sqrt{3-\sqrt5}}\)
\(=\sqrt2\left(\frac{3+\sqrt5}{4+\sqrt{6+2\sqrt5}}+\frac{3-\sqrt5}{4-\sqrt{6-2\sqrt5}}\right)\)
\(=\sqrt2\left(\frac{3+\sqrt5}{4+\sqrt{\left(\sqrt5+1\right)^2}}+\frac{3-\sqrt5}{4-\sqrt{\left(\sqrt5-1\right)^2}}\right)\)
\(=\sqrt2\left(\frac{3+\sqrt5}{4+\left(\sqrt5+1\right)^{}}+\frac{3-\sqrt5}{4-\left(\sqrt5-1\right)^{}}\right)\)
\(=\sqrt2\left(\frac{3+\sqrt5}{4+\sqrt5+1^{}}+\frac{3-\sqrt5}{4-\sqrt5+1^{}}\right)=\sqrt2\left(\frac{3+\sqrt5}{5+\sqrt5^{}}+\frac{3-\sqrt5}{5-\sqrt5^{}}\right)\)
\(=\frac{1}{\sqrt2}\left(\frac{2\left(3+\sqrt5\right)}{5+\sqrt5}+\frac{2\left(3-\sqrt5\right)}{5-\sqrt5}\right)=\frac{1}{\sqrt2}\cdot\left(\frac{6+2\sqrt5}{5+\sqrt5}+\frac{6-2\sqrt5}{5-\sqrt5}\right)\)
\(=\frac{1}{\sqrt2}\left(\frac{\left(\sqrt5+1\right)^2}{\sqrt5\left(\sqrt5+1\right)}+\frac{\left(\sqrt5-1\right)^2}{\sqrt5\left(\sqrt5-1\right)}\right)=\frac{1}{\sqrt2}\cdot\frac{\sqrt5+1+\sqrt5-1}{\sqrt5}=\frac{1}{\sqrt2}\cdot2=\sqrt2\)
c: \(C=\sqrt{4+\sqrt{10+2\sqrt5}}+\sqrt{4-\sqrt{10+2\sqrt5}}\)
=>\(C^2=4+\sqrt{10+2\sqrt5}+4-\sqrt{10+2\sqrt5}+2\cdot\sqrt{4^2-\left(10+2\sqrt5\right)}\)
=>\(C^2=8+2\cdot\sqrt{16-10-2\sqrt5}=8+2\cdot\sqrt{6-2\sqrt5}\)
=>\(C^2=8+2\cdot\left(\sqrt5-1\right)=6+2\sqrt5=\left(\sqrt5+1\right)^2\)
=>\(C=\sqrt5+1\)
f: \(F=\sqrt[3]{26+15\sqrt3}-\sqrt[3]{26-15\sqrt3}\)
\(=\sqrt[3]{2^3+3\cdot2^2\cdot\sqrt3+3\cdot2\cdot\left(\sqrt3\right)^2+3\sqrt3}-\sqrt[3]{2^3-3\cdot2^2\cdot\sqrt3+3\cdot2\cdot\left(\sqrt3\right)^2-3\sqrt3}\)
\(=\sqrt[3]{\left(2+\sqrt3\right)^3}-\sqrt[3]{\left(2-\sqrt3\right)^3}=2+\sqrt3-\left(2-\sqrt3\right)=2\sqrt3\)