 giúp mk 2 bài này vs ạ
giúp mk 2 bài này vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì \(AB//CD\) nên \(\left\{{}\begin{matrix}\widehat{B}+\widehat{C}=180^0\\\widehat{A}+\widehat{D}=180^0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\widehat{B}=\left(180^0+40^0\right):2=110^0\\3\widehat{D}=180^0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{C}=180^0-110^0=70^0\\\widehat{D}=60^0\end{matrix}\right.\Rightarrow\widehat{A}=120^0\)
\(\widehat{B}=110^0\)
\(\widehat{C}=70^0\)
\(\widehat{A}=120^0\)
\(\widehat{D}=60^0\)

2,Có \(\widehat{A}+\widehat{D}=180^0\) (Hai góc trong cùng phía do AB//CD)
\(\Rightarrow\widehat{D}=180^0-115^0=65^0\)

Em ơi em chụp lại đề bài sáng và rõ chữ hơn, hoặc em đánh văn bản ra nhé

\(a.n_{Zn}=\dfrac{6,5}{65}=0,1\left(mol\right)\\ Zn+2HCl\rightarrow ZnCl_2+H_2\\ b.0,1........0,2..........0,1.........0,1\left(mol\right)\\ C\%_{ddH_2SO_4}=\dfrac{0,1.98}{140}.100=7\%\\ c.m_{dd.muối}=6,5+140-0,1.2=146,3\left(g\right)\\ C\%_{ddZnCl_2}=\dfrac{136.0,1}{146,3}.100\approx9,296\%\\ \)
a.nZn=6,565=0,1(mol)Zn+2HCl→ZnCl2+H2b.0,1........0,2..........0,1.........0,1(mol)C%ddH2SO4=0,1.98140.100=7%c.mdd.muối=6,5+140−0,1.2=146,3(g)C%ddZnCl2=136.0,1146,3.100≈9,296%


a: Ta có: AH\(\perp\)BD
CK\(\perp\)BD
Do đó: AH//CK
b: Xét ΔADH vuông tại H và ΔCBK vuông tại K có
AD=CB
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔADH=ΔCBK
Suy ra: AH=CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành
Suy ra: AK//CH

30: Ta có: \(5x-5y+ax-ay\)
\(=5\left(x-y\right)+a\left(x-y\right)\)
\(=\left(x-y\right)\left(a+5\right)\)
31: Ta có: \(6x^2-11x+3\)
\(=6x^2-9x-2x+3\)
\(=\left(2x-3\right)\left(3x-1\right)\)

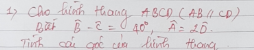
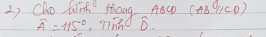




 Giúp mk lm bài này vs ạ
Giúp mk lm bài này vs ạ
3.5:
Xét `\DeltaCID` có:
`\hat{IDC}+\hat{ICD}+\hat{CID}=180^o`
`\hat{IDC}+\hat{ICD}=180^o-\hat{CID}`
`\hat{IDC}+\hat{ICD}=180^o-105^o=75^o`
Mà: `ID,IC` lần lượt là phân giác của `\hat{D},\hat{D}
Suy ra: `\hat{D}=2\hat{IDC},\hat{C}=2\hat{ICD}`
`->1/2\hat{D}+1/2\hat{C}=75^o`
`->\hat{D}+\hat{C}=75^o*2=150^o`
Xét tứ giác `ABCD` có:
`\hat{A}+\hat{B}+\hat{C}+\hat{D}=360^o`
`->\hat{A}+\hat{B}=360^o-(\hat{C}+\hat{D})`
`->\hat{A}+\hat{B}=360^o-150^o`
`->\hat{A}+\hat{B}=210^o`
`->\hat{A}=210^o-\hat{B}`
Mà: `\hat{A}-\hat{B}=30^o`
`->210^o-\hat{B}-\hat{B}=30^o`
`->2\hat{B}=210^o-30^o=180^o`
`->\hat{B}=180^o/2=90^o`
Suy ra: `\hat{A}=210^o-90^o=120^o`
3.5:
Xét ΔCID có \(\hat{ICD}+\hat{IDC}+\hat{CID}=180^0\)
=>\(\hat{ICD}+\hat{IDC}=180^0-105^0=75^0\)
=>\(\frac12\left(\hat{BCD}+\hat{CDA}\right)=75^0\)
=>\(\hat{BCD}+\hat{CDA}=75^0\cdot2=150^0\)
Xét tứ giác ABCD có \(\hat{BAD}+\hat{ABC}+\hat{BCD}+\hat{CDA}=360^0\)
=>\(\hat{BAD}+\hat{ABC}=360^0-150^0=210^0\)
mà \(\hat{BAD}-\hat{ABC}=30^0\)
nên \(\hat{BAD}=\frac{210^0+30^0}{2}=120^0;\hat{ABC}=120^0-30^0=90^0\)
3.4:
Xét tứ giác ABCD có \(\hat{BAD}+\hat{ABC}+\hat{BCD}+\hat{ADC}=360^0\)
=>\(\hat{BCD}+\hat{ADC}=360^0-\left(\hat{BAD}+\hat{ABC}\right);\hat{BAD}+\hat{ABC}=360^0-\left(\hat{BCD}+\hat{ADC}\right)\)
Xét ΔEAB có \(\hat{EAB}+\hat{EBA}+\hat{AEB}=180^0\)
=>\(\hat{BEA}+\frac12\left(\hat{BAD}+\hat{ABC}\right)=180^0\)
=>\(\hat{BEA}+\frac12\left\lbrack360^0-\left(\hat{ADC}+\hat{BCD}\right)\right\rbrack=180^0\)
=>\(\hat{BEA}+180^0-\frac12\left(\hat{ADC}+\hat{BCD}\right)=180^0\)
=>\(\hat{BEA}=180^0-180^0+\frac12\left(\hat{ADC}+\hat{BCD}\right)=\frac12\left(\hat{ADC}+\hat{BCD}\right)\)
Vì AE và AF là hai tia phân giác của hai góc kề bù
nên AE⊥AF
Vì BF,BE là hai tia phân giác của hai góc kề bù
nên BF⊥BE
Xét tứ giác FAEB có \(\hat{FAE}+\hat{FBE}+\hat{AFB}+\hat{AEB}=360^0\)
=>\(\hat{AFB}+\hat{AEB}=360^0-90^0-90^0=180^0\)
=>\(\hat{AFB}=180^0-\frac12\left(\hat{ADC}+\hat{BCD}\right)=\frac12\left(360^0-\hat{ADC}-\hat{BCD}\right)=\frac12\cdot\left(\hat{BAD}+\hat{ABC}\right)\)