
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Khi m=2 thì \(y=\left(2\cdot2-1\right)x-2^2+2=3x-2\)
Phương trình hoành độ giao điểm là:
\(x^2-3x+2=0\)
=>x=2 hoặc x=1
Khi x=2 thì y=4
Khi x=1 thì y=1
c: Phương trình hoành độ giao điểm là:
\(x^2-\left(2m-1\right)x+m^2-2=0\)
\(\text{Δ}=\left(2m-1\right)^2-4\left(m^2-2\right)\)
\(=4m^2-4m+1-4m^2+8=-4m+9\)
Để (P) cắt (d) tại hai điểm phân biệt thì -4m+9>0
=>-4m>-9
hay m<9/4

a: Để hai đường thẳng song song thì 2m+1=2
hay m=1/2

b: Để hai đường thẳng song song thì 2m+1=2
hay m=1/2

Hàm số y = 2x + 3k có các hệ số a = 2, b = 3k.
Hàm số y = (2m + 1)x + 2k – 3 có các hệ số a' = 2m + 1, b' = 2k – 3.
Hai hàm số đã cho là hàm số bậc nhất nên 2m + 1 ≠ 0
![]()
a) Hai đường thẳng cắt nhau khi a ≠ a' tức là:
2 ≠ 2m + 1 ⇔ 2m ≠ 1

b) Hai đường thẳng song song với nhau khi a = a' và b ≠ b' tức là:
2 = 2m + 1 và 3k ≠ 2k – 3

c) Hai đường thẳng trùng nhau khi a = a' và b = b' tức là:
2 = 2m + 1 và 3k = 2k – 3
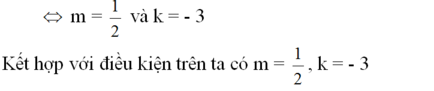

Hai đường thẳng trùng nhau khi a = a' và b = b' tức là:
2 = 2m + 1 và 3k = 2k – 3
HT

Hàm số y = 2x + 3k có các hệ số a = 2, b = 3k.
Hàm số y = (2m + 1)x + 2k – 3 có các hệ số a' = 2m + 1, b' = 2k – 3.
Hai hàm số đã cho là hàm số bậc nhất nên 2m + 1 ≠ 0
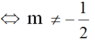
Hai đường thẳng cắt nhau khi a ≠ a' tức là:
2 ≠ 2m + 1 ⇔ 2m ≠ 1

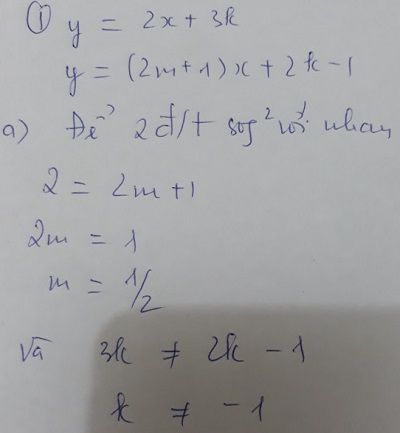 câu a đây mong bạn tham thảo
câu a đây mong bạn tham thảo
Để (d1) cắt (d2) thì \(\frac{m}{2m}<>\frac{m-1}{m+1}\)
=>\(\frac{m-1}{m+1}<>\frac12\)
=>\(\frac{m-1}{m+1}-\frac12<>0\)
=>\(\frac{2m-2-m-1}{2\left(m+1\right)}<>0\)
=>\(\frac{m-3}{m+1}<>0\)
=>\(\begin{cases}m-3<>0\\ m+1<>0\end{cases}\Rightarrow m\notin\left\lbrace3;-1\right\rbrace\)
Để (d1)//(d2) thì \(\frac{m}{2m}=\frac{m-1}{m+1}<>\frac{3m+4}{m-4}\)
=>\(\begin{cases}\frac{m-1}{m+1}=\frac12\\ \frac{3m+4}{m-4}<>\frac12\end{cases}\Rightarrow\begin{cases}2\left(m-1\right)=m+1\\ \frac{3m+4}{m-4}<>\frac12\end{cases}\)
=>\(\begin{cases}2m-2=m+1\\ \frac{3m+4}{m-4}<>\frac12\end{cases}\Rightarrow\begin{cases}m=3\\ \frac{3m+4}{m-4}<>\frac12\end{cases}\)
=>m=3
Để (d1) trùng với (d2) thì \(\frac{m}{2m}=\frac{m-1}{m+1}=\frac{3m+4}{m-4}\)
=>\(\frac{m-1}{m+1}=\frac{3m+4}{m-4}=\frac12\)
=>2(m-1)=m+1 và 2(3m+4)=m-4
=>2m-2=m+1 và 6m+8=m-4
=>m=3 và 5m=-12
=>m∈∅