Cho hình thang ABCD có đáy AB = 1/2 CD; AC và BD cắt nhau tại I. a) So sánh diện tích tam giác ABC và diện tích tam giác BDC. b) So sánh diện tích các cặp hình tam giác: ABC và ABD, ACD và BCD, AID và BIC c) Kéo dài DA về phía A và CB về phía B, chúng cắt nhau tại K. Tìm tỉ số AK và AD.
Ai giải đúng mình sẽ tick cho. 100% uy tín

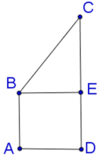
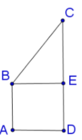
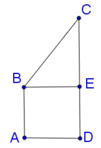

a: Kẻ BH⊥CD tại H, CM⊥AB tại M
=>BH,CM là các đường cao của hình thang ABCD
Vì BH là đường cao của hình thang ABCD
nên \(S_{ABCD}=\frac12\times BH\times\left(AB+CD\right)\left(1\right)\)
Vì CM là đường cao của hình thang ABCD
nên \(S_{ABCD}=\frac12\times CM\times\left(AB+CD\right)\left(2\right)\)
Từ (1),(2) suy ra BH=CM(3)
Xét ΔBDC có BH là đường cao
nên \(S_{BDC}=\frac12\times BH\times DC\left(4\right)\)
Xét ΔABC có CM là đường cao
nên \(S_{ABC}=\frac12\times CM\times AB\left(5\right)\)
Từ (3),(4),(5) suy ra \(\frac{S_{BDC}}{S_{ABC}}=\frac{DC}{AB}=2\)
=>\(S_{BDC}>S_{ABC}\)
b: Kẻ DE⊥AB vuông tại E
=>DE là đường cao của hình thang ABCD
=>\(S_{ABCD}=\frac12\times DE\times\left(AB+CD\right)\) (6)
từ (1),(2),(6) suy ra BH=DE=CM
Xét ΔBAD có DE là đường cao
nên \(S_{DAB}=\frac12\times DE\times AB\) (7)
Xét ΔABC có CM là đường cao
nên \(S_{ABC}=\frac12\times CM\times AB\) (8)
Từ (7),(8) suy ra \(\frac{S_{DAB}}{S_{ABC}}=\frac{DE}{CM}=1\)
=>\(S_{ABD}=S_{ABC}\)
Kẻ AF⊥DC tại F
=>AF là đường cao của hình thang ABCD
=>\(S_{ABCD}=\frac12\times FA\times\left(AB+CD\right)\) (9)
Từ (1),(2),(6),(9) suy ra FA=ED=BH=CM
=>AF=BH(10)
Xét ΔADC có AF là đường cao
nên \(S_{ADC}=\frac12\times FA\times DC\left(11\right)\)
Xét ΔBCD có BH là đường cao
nên \(S_{BDC}=\frac12\times BH\times CD\) (12)
Từ (10),(11),(12) suy ra \(S_{ADC}=S_{BDC}\)
=>\(S_{ADC}-S_{DIC}=S_{BDC}-S_{DIC}\)
=>\(S_{AID}=S_{BIC}\)
c: Vì AB//CD
nên \(\frac{KA}{KD}=\frac{AB}{CD}=\frac12\)
=>A là trung điểm của KD
=>KA=AD
=>\(\frac{AK}{AD}=1\)
a) Diện tích của tam giác ABC và tam giác BDC có thể được so sánh thông qua chiều cao tương ứng từ các đỉnh A và D xuống đáy CD. Vì AB = 1/2 CD, nên diện tích tam giác ABC sẽ nhỏ hơn diện tích tam giác BDC. Cụ thể, diện tích tam giác ABC = 1/2 * AB * h1 và diện tích tam giác BDC = 1/2 * CD * h2. Với h1 = h2 (chiều cao từ A và D xuống CD), ta có diện tích tam giác ABC < diện tích tam giác BDC.
b) So sánh diện tích các cặp hình tam giác:
c) Khi kéo dài DA về phía A và CB về phía B, chúng cắt nhau tại K. Tỉ số AK và AD sẽ bằng tỉ số của các đoạn thẳng tương ứng trên cùng một đường thẳng. Do đó, tỉ số AK/AD = 2 (vì AB = 1/2 CD)
nhớ tick nha :)))