làm thế nào để nhận biết và chứng minh hai đường thẳng song ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CW
25 tháng 8 2016
CM 2 đường thẳng vuông góc:
1. Định lý: Nếu 1 đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
2. CM 2 đường thẳng đó tạo thành 1 góc 90o.
v..v....
CM 2 đường thẳng song song:
1. CM 2 đường thẳng đó cùng vuông góc với 1 đường thẳng thứ ba
2. CM 2 góc sole trong/ đồng vị/ sole ngoài bằng nhau
3. CM 2 góc trong cùng phía/ ngoài cùng phía bù nhau
25 tháng 8 2016
các bn hiu nhầm câu hoi rùì
giả sử có 2 dg thg xy và cd, trên xy lấy AB,trên cd lay CD =AB
neu AD = BC thi chac chan xy//cd ( vi ABCD la hbh)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
a) Qua điểm \(A\), ta vẽ được duy nhất một đường thẳng \(a\) song song với đường thẳng \(a'\).
Qua điểm \(A\), ta vẽ được duy nhất một đường thẳng \(b\) song song với đường thẳng \(b'\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}a\parallel a'\\a' \subset \left( Q \right)\end{array} \right\} \Rightarrow a\parallel \left( Q \right)\\\left. \begin{array}{l}b\parallel b'\\b' \subset \left( Q \right)\end{array} \right\} \Rightarrow b\parallel \left( Q \right)\end{array}\)
b) Ta có:
\(\left. \begin{array}{l}a\parallel \left( Q \right)\\b\parallel \left( Q \right)\\a,b \subset mp\left( {a,b} \right)\end{array} \right\} \Rightarrow mp\left( {a,b} \right)\parallel \left( Q \right)\)
6 tháng 9 2016
- Hai đường thẳng cùng thẳng góc với đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.
- Một đường thẳng cắt hai đường thẳng mà trong các góc tạo thành có các cặp góc: Đồng vị hay so le trong bằng nhau thì hai đường thẳng bị cắt là hai đường thẳng song song.
- Một đường thẳng cắt hai đường thẳng và định ra trên hai đường thẳng đó những đoạn thẳng tương ứng tỷ lệ bằng nhau, thì hai đường thẳng đó song song nhau.
- Hai đường thẳng cùng song song với một đường thẳng thứ ba, thì hai đường thẳng đó song song nhau.
6 tháng 9 2016
Hai đường thẳng song song là hai đường thẳng đối diện nhau
Ko có điểm chung nào
MA
24 tháng 8 2016
ta chứng minh nó là đồng vị,
kề bù,so le trong ,
trong cùng phía, ngoài cùng phía
từ đó ta sẽ pt hai đường thẳng đó có song song hay là vuông góc hay không
tíc mình nha
18 tháng 9 2023
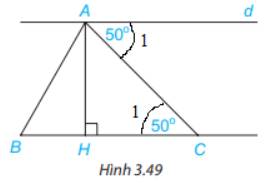
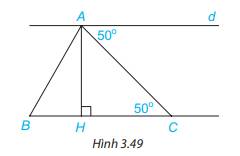
a) Vì \(\widehat {{A_1}} = \widehat {{C_1}}( = 50^\circ )\), mà 2 góc này ở vị trí so le trong nên d // BC (Dấu hiệu nhận biết hai đường thẳng song song )
b) Vì d // BC, mà AH \( \bot \)BC nên d \( \bot \)BC (Đường thẳng vuông góc với một trong hai đường thẳng song song thì cũng vuông góc với đường thẳng kia)
c) Trong các kết luận trên, kết luận a) được suy ra từ dấu hiệu nhận biết hai đường thẳng song song
Kết luận b) được suy ra từ tính chất của hai đường thẳng song song.
CM
24 tháng 10 2018
Muốn kiểm tra hai đường thẳng a và b có song song với nhau hay không ta vẽ đường thẳng c cắt 2 đường thẳng a và b rồi đo 1 cặp góc so le trong xem chúng có bằng nhau không. Nếu có cặp góc so le trong bằng nhau thì a//b
Có thể thay cặp góc so le trong bằng các cặp góc đồng vị hoặc cặp góc trong cùng phía. Cặp góc đồng vị bằng nhau thì a//b; cặp góc trong cùng phía bù nhau thì a//b.
Cũng có thể dùng eke kẻ đường thẳng c vuông góc với a rồi kiểm tra xem đường thẳng đó có vuông góc với b không. Nếu c vuông góc với b thì a//b
9 tháng 5 2018
Giải:
- Muốn kiểm tra hai đường thẳng a. B có song song với nhau hay không ta vẽ đường thẳng c cắt 2 đường thẳng a và b rồi đo 1 cặp góc so le trong xem chúng có bằng nhau không. Nếu có cặp góc so le trong bằng nhau thì a//b
- Có thể thay cặp góc so le trong bằng các cặp góc đồng vị hoặc cặp góc trong cùng phía.
- Cũng có thể dùng eke kẻ đường thẳng vuông góc với a rồi kiểm tra xem đường thẳng đo có vuông góc với b không
AW
9 tháng 5 2018
Hai đường // có :
- Hai góc cùng phía bù nhau
- Hai góc so le trong bằng nhau
- Hai góc đồng vị bằng nhau
Đúng nha. Bạn yên tâm
Tk mk nha. Chúc bạn học giỏi
WJ
13 tháng 10 2015
-Nếu một đường thẳng cắt 2 đường thẳng phân biệt mà:
+Có cặp góc so le trong bằng nhau
+Có cặp góc đồng vị bằng nhau
+Có cặp góc trong cùng phía bù nhau (90o)
thì hai đường thẳng phân biệt đó bằng nhau.
1. Dựa vào góc
2. Dựa vào quan hệ hình học
3. Dựa vào tọa độ (nếu có)