Cho tam giác ABC có góc A = 90°. Kẻ AH vuông góc với BC ( H thuộc BC ). Chứng minh AB+AC<BC+AH.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TC
Thầy Cao Đô
Giáo viên
VIP
27 tháng 12 2022
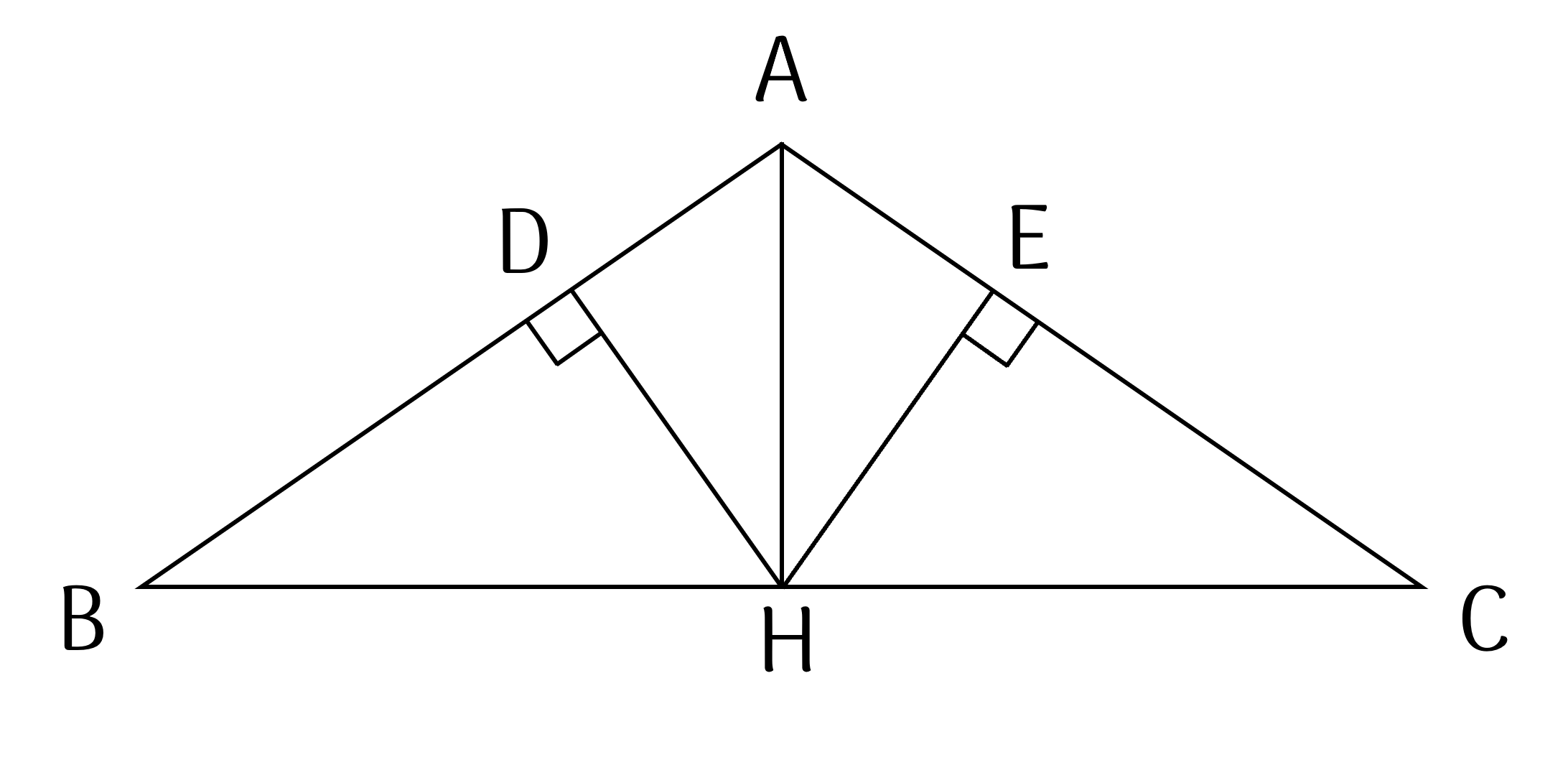
a) Xét hai tam giác vuông $AHB$ và $AHC$ có:
$AH$ là cạnh chung;
$AB = AC$ (gt);
Suy ra $\Delta AHB=\Delta AHC$ (cạnh huyền - cạnh góc vuông)
Suy ra $HB = HC$ (Hai cạnh tương ứng)
$\widehat{BAH} = \widehat{CAH}$ (hai góc tương ứng).
b) Xét hai tam giác vuông $ADH$ và $AEH$ có:
$AH$ là cạnh chung;
$\widehat{BAH} = \widehat{CAH}$ (cmt);
Suy ra $\Delta ADH=\Delta AEH$ (cạnh huyền - góc nhọn).
Suy ra $HD = HE$ (Hai cạnh tương ứng) nên $\Delta HDE$ cân tại $H$.
5 tháng 4 2022
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
hay HB=HC
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác
hay \(\widehat{BAH}=\widehat{CAH}\)
b: BH=CH=BC/2=4(cm)
nên AH=3(cm)
c: Xét ΔAEH vuông tại E và ΔADH vuông tại D có
AH chung
\(\widehat{EAH}=\widehat{DAH}\)
DO đó: ΔAEH=ΔADH
Suy ra: HE=HD
hay ΔHDE cân tại H
KB
9 tháng 5 2021
a) Chứng minh HB=HC: Xét ΔAHB và ΔAHC có: ∠AHB=∠AHC=90(độ) AH cạnh chung AB=AC(gt) ⇒ ΔAHB = ΔAHC (ch-cgv) ⇒ HB=HC (2 cạnh tương ứng)
b) Ta có: HB=HC=BC/2=6/2=3(cm) Ta có: ΔAHB vuông tại H. ⇒ AH(mũ 2)+BH(mũ 2)=AB(mũ 2) ⇒ AH(mũ 2)=AB(mũ 2)-BH(mũ 2) =4(mũ 2)-3(mũ 2)=16-9=7 ⇒ AH=√7(cm)
c) Ta có: ΔAHB = ΔAHC ⇒ ∠BAH=∠CAH Xét ΔAHD và ΔAHE có: ∠D=∠E=90(độ) AH cạnh chung ∠BAH=∠CAH (gt) ⇒ ΔAHD = ΔAHE (ch-gn) ⇒ DH=EH ⇒ ΔHDE cân tại H. A B C H D E
12 tháng 7 2023
Xét ΔABM vuông tại M và ΔACM vuông tại M có
AB=AC
AM chung
=>ΔABM=ΔACM
=>MB=MC
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
góc HAM=góc KAM
=>ΔAHM=ΔAKM
=>AH=AK
Xét ΔABC có AH/AB=AK/AC
nên HK//BC
OP
6 tháng 2 2022
a.ta có trong tam giác cân ABC đường cao cũng là đường trung tuyến => HB = HC
b.áp dụng định lý pitago ta có:
\(AB^2=AH^2+HB^2\)
\(5^2=AH^2+\left(8:2\right)^2\)
\(AH=\sqrt{5^2-4^2}=3cm\)
c.Xét tam giác vuông BHD và tam giác vuông CHE, có:
BH = CH ( cmt )
góc B = góc C ( ABC cân )
Vậy tam giác vuông BHD = tam giác vuông CHE
=> HD = HE
=> HDE cân tại H
d.ta có AB = AD + DB
AC = AE + EC
Mà BD = CE ( 2 cạnh tương ứng của 2 tam giác bằng nhau )
=> AD = AE
=> ADE cân tại A
Mà A là đường cao cũng là đường trung trực trong tam giác cân ABC cũng là đường trung trực của tam giác cân ADE ( cmx )
Chúc bạn học tốt !!!!
23 tháng 6 2022
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểmcủa BC
hay HB=HC
b: Xét ΔADH vuông tạiD và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra HD=HE
hay ΔHDE cân tại H
9 tháng 2 2021
a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
⇔BH=CH(hai cạnh tương ứng)
b) Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(BH^2+AH^2=AB^2\)
\(\Leftrightarrow BH^2=AB^2-AH^2=5^2-4^2=9\)
hay BH=3(cm)
Vậy: BH=3cm
c) Ta có: ΔABH=ΔACH(cmt)
nên \(\widehat{BAH}=\widehat{CAH}\)(hai góc tương ứng)
hay \(\widehat{DAH}=\widehat{EAH}\)
Xét ΔDAH vuông tại D và ΔEAH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)(cmt)
Do đó: ΔDAH=ΔEAH(cạnh huyền-góc nhọn)
Suy ra: AD=AE(hai cạnh tương ứng)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
S
15 tháng 2
a. △ABC cân tại A, lại có AH là đường cao
=> AH cũng là đường trung tuyến, đường phân giác
=> HB = HC và \(\widehat{BAH}=\widehat{CAH}\)
b. ta có: \(HB=\dfrac{1}{2}BC=\dfrac{1}{2}\cdot6=3\left(cm\right)\)
áp dụng định lý pythagore vào △BAH vuông tại H ta có:
\(AH=\sqrt{AB^2-BH^2}=\sqrt{4^2-3^2}=\sqrt{7}\left(cm\right)\)
c. xét △ vuông HMB và △ vuông HNC có
HB = HC (gt); \(\widehat{ABC}=\widehat{ACB}\) (△ABC cân tại A)
=> △HMB = △HNC (ch-gn)
=> HM = HN (2 cạnnh tương ứng)
=> △MHN là △ cân (tại H)
NH
25 tháng 10 2019
A B C H D ︵ 30 o
a, Vì BAC = 90o
=> BA ⊥ AC
Mà HD ⊥ AB (gt)
=> AC // HD (từ vuông góc đến song song)
b, Vì AC // HD (cmt) => BHD = HCA = 30o
Vì AH ⊥ BC (gt) => AHB = 90o
Xét △BDH vuông tại D có: DBH + BHD = 90o (tổng 3 góc trong tam giác)
=> DBH + 30o = 90o
=> DBH = 60o
Xét △BAH vuông tại H có: BAH + ABH = 90o
=> BAH + 60o = 90o
=> BAH = 30o
ΔABC vuông tại A
=>\(S_{ABC}=\frac12\cdot AB\cdot AC\left(1\right)\)
ΔABC có AH là đường cao
nên \(S_{ABC}=\frac12\cdot AH\cdot BC\left(2\right)\)
Từ (1),(2) suy ra \(AH\cdot BC=AB\cdot AC\)
\(\left(AB+AC\right)^2-\left(BC+AH\right)^2\)
\(=AB^2+AC^2+2\cdot AB\cdot AC-\left(BC^2+2\cdot BC\cdot AH+AH^2\right)\)
\(=\left(AB^2+AC^2-BC^2\right)+\left(2\cdot AB\cdot AC-2\cdot AH\cdot BC\right)-AH^2\)
\(=-AH^2<0\)
=>\(\left(AB+AC\right)^2<\left(AH+BC\right)^2\)
=>AB+AC<AH+BC
Ta có đề bài:
AB + AC < BC + AH
]
🧠 Phân tích bài toán:
\(A B + A C < B C + A H\)
✍️ Chứng minh:
⚙ Ý tưởng:
So sánh tổng hai cạnh góc vuông \(A B + A C\) với tổng đường cao và cạnh huyền \(A H + B C\)
🔹 Xét tam giác vuông \(\triangle A B C\):
Trong tam giác vuông, tổng hai cạnh góc vuông nhỏ hơn tổng cạnh huyền và đường cao kẻ từ đỉnh vuông góc:
AB + AC < BC + AH
]
Luôn đúng với tam giác ABC vuông tại A, với \(H\) là chân đường cao từ A.
📌 Cách chứng minh (suy luận hình học):
AH < AB \quad \text{và} \quad AH < AC
]
(Vì trong tam giác vuông, đường cao nhỏ hơn hai cạnh góc vuông trừ khi là tam giác đều – không xảy ra ở đây)
BC > AB, \quad BC > AC
]
BC + AH > AB \quad \text{và} \quad BC + AH > AC
\Rightarrow BC + AH > AB + AC
]
✅ Kết luận:
\(\boxed{A B + A C < B C + A H}\)
Đẳng thức không xảy ra, vì không thể có tam giác vuông nào mà hai cạnh góc vuông bằng tổng cạnh huyền và đường cao.
Nếu em cần vẽ hình minh họa hoặc chứng minh bằng tọa độ, cô có thể hướng dẫn thêm nha! 🎓