tìm cặp số nguyên (x;y) để biểu thức M = (xy + x + 1)/(xy + y + 2) có giá trị nguyên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
4
NH
13 tháng 2 2019
\(\left(3x-5\right)⋮\left(x+2\right)\)
\(\Rightarrow3.\left(x+2\right)-11⋮\left(x+2\right)\)
Vì \(3.\left(x+2\right)⋮\left(x+2\right)\)
\(\Rightarrow11⋮\left(x+2\right)\)
\(\Rightarrow\left(x+2\right)\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
Tự lập bảng :) T lười qá
NH
2
AM
20 tháng 6 2015
\(P=\frac{x-2}{x+1}=\frac{x+1}{x+1}-\frac{3}{x+1}=1-\frac{3}{x+1}\)
P nguyên <=>3 chia hết cho x+1 <=>x+1 là Ư(3)
Mà Ư(3)={+-1;+-3}
Ta có bảng sau:
| x+1 | 1 | -1 | 3 | -3 |
| x | 0 | -2 | 2 | -4 |
Vậy x={-4;-2;0;2} thì P nguyên
20 tháng 6 2015
p nguyên <=> x-2=x+1-3 chia hết cho x+1 => 3 chia hết cho x+1 => x+1 thuộc Ư(3) =>x+1 thuộc {-3;-1;1;3} <=> x thuộc {-4;-2;0;2}
13 tháng 1 2019
Bài 2: Giả sử tồn tại x,y nguyên dương t/m đề, khi đó pt cho tương đương:
\(4x^2+4y^2-12x-12y=0\Leftrightarrow\left(2x+3\right)^2+\left(2y+3\right)^2=18\)
Ta thấy: \(18=9+9=3^2+3^2\). Mà x,y thuộc Z+ nên \(\hept{\begin{cases}2x+3=3\\2y+3=3\end{cases}\Leftrightarrow}\hept{\begin{cases}x=0\\y=0\end{cases}}\)
Vậy cặp nghiệm nguyên t/m pt là (x;y) = (0;0)
13 tháng 1 2019
Làm lại bài 2 :v (P/S: Bạn bỏ bài kia đi nhé)
\(4x^2+4y^2-12x-12y=0\Leftrightarrow\left(2x-3\right)^2+\left(2y-3\right)^2=18\)
Ta thấy: \(18=9+9=3^2+3^2\). Mà x,y thuộc Z+ nên \(\hept{\begin{cases}2x-3=3\\2y-3=3\end{cases}\Leftrightarrow}\hept{\begin{cases}x=3\\y=3\end{cases}}\)
Vậy (x;y) = (3;3)
XO
6 tháng 8 2020
\(B=\frac{1}{x-y}:\frac{x+2}{2\left(x-y\right)}=\frac{1}{x-y}.\frac{2\left(x-y\right)}{x+2}=\frac{2}{x+2}\)
Để B là số nguyên
=> \(\frac{2}{x+2}\)là số nguyên
=> \(2⋮x+2\)
=> \(x+2\inƯ\left(2\right)\)
=> \(x+2\in\left\{1;-1;2;-2\right\}\)
=> \(x\in\left\{-1;-3;0;-4\right\}\)
Vậy các cặp (x ;y) thỏa mãn là (-1 ; y) ; (-3 ; y) ; (0 ; y) ; (-4 ; y) với mọi y nguyên
NA
2
21 tháng 4 2021
\(x^2-xy+y+1=0\)
\(\Leftrightarrow\left(x^2-1\right)-y\left(x-1\right)+2=0\)
\(\Leftrightarrow\left(x+1-y\right)\left(x-1\right)=-2\)
\(\Rightarrow x-1;x+1-y\inƯ\left(-2\right)=\left\{\pm1;\pm2\right\}\)
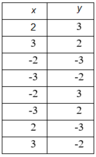
| x - 1 | 1 | -1 | 2 | -2 |
| x + 1 - y | 2 | -2 | 1 | -1 |
| x | 2 | 0 | 3 | -1 |
| y | 1 | 3 | 3 | 1 |
21 tháng 4 2021
bảng mình xét nhầm nhé phải là như này :
| x - 1 | 1 | -1 | 2 | -2 |
| x + 1 - y | -2 | 2 | -1 | 1 |
| x | 2 | 0 | 3 | -1 |
| y | 5 | -1 | 5 | 1 |
PT
2
TM
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
18 tháng 12 2023
\(x\) - 1.y = 7
\(x\) - y = 7
\(x\) = 7 + y (y \(\in\) Z)
9 tháng 10 2018
Giả sử (x;y) là cặp số nguyên dương cần tìm. Khi đó ta có:
(xy-1) I (x^3+x) => (xy-1) I x.(x^2+1) (1)
Do (x; xy-1) =1 ( Thật vậy: gọi (x;xy-1) =d => d I x => d I xy => d I 1).
Nên từ (1) ta có:
(xy-1) I (x^2+1)
=> (xy-1) I (x^2+1+xy -1) => (xy-1) I (x^2+xy) => (xy-1) I x.(x+y) => (xy-1) I (x+y)
Điều đó có nghĩa là tồn tại z ∈ N* sao cho:
x+y = z(xy-1) <=> x+y+z =xyz (2)
[Đây lại có vẻ là 1 bài toán khác]
Do vai trò bình đẳng nên ta giả sử: x ≥ y ≥ z.
Từ (2) ta có: x+y+z ≤ 3x => 3x ≥ xyz => 3 ≥ yz ≥ z^2 => z=1
=> 3 ≥ y => y ∈ {1;2;3}
Nếu y=1: x+2 =x (loại)
Nếu y=2: (2) trở thành x+3 =2x => x=3
Nếu y=3: x+4 = 3x => x=2 (loại vì ta có x≥y)
Vậy khi x ≥ y ≥ z thì (2) có 1 nghiệm (x;y;z) là (3;2;1)
Hoán vị vòng quanh được 6 nghiệm là: .....[bạn tự viết nhé]
Vậy bài toán đã cho có 6 nghiệm (x;y) là : .... [viết y chang nhưng bỏ z đi]
KS
9 tháng 10 2018
Giả sử (x;y) là cặp số nguyên dương cần tìm. Khi đó ta có:
(xy-1) I (x^3+x) => (xy-1) I x.(x^2+1) (1)
Do (x; xy-1) =1 ( Thật vậy: gọi (x;xy-1) =d => d I x => d I xy => d I 1).
Nên từ (1) ta có:
(xy-1) I (x^2+1)
=> (xy-1) I (x^2+1+xy -1) => (xy-1) I (x^2+xy) => (xy-1) I x.(x+y) => (xy-1) I (x+y)
Điều đó có nghĩa là tồn tại z ∈ N* sao cho:
x+y = z(xy-1) <=> x+y+z =xyz (2)
[Đây lại có vẻ là 1 bài toán khác]
Do vai trò bình đẳng nên ta giả sử: x ≥ y ≥ z.
Từ (2) ta có: x+y+z ≤ 3x => 3x ≥ xyz => 3 ≥ yz ≥ z^2 => z=1
=> 3 ≥ y => y ∈ {1;2;3}
Nếu y=1: x+2 =x (loại)
Nếu y=2: (2) trở thành x+3 =2x => x=3
Nếu y=3: x+4 = 3x => x=2 (loại vì ta có x≥y)
Vậy khi x ≥ y ≥ z thì (2) có 1 nghiệm (x;y;z) là (3;2;1)
Hoán vị vòng quanh được 6 nghiệm là: .....[bạn tự viết nhé]
Vậy bài toán đã cho có 6 nghiệm (x;y) là : .... [viết y chang nhưng bỏ z đi]
Chúng ta cần tìm cặp số nguyên \(\left(\right. x ; y \left.\right)\) sao cho biểu thức
\(M = \frac{x y + x + 1}{x y + y + 2}\)
có giá trị là số nguyên.
Bước 1: Viết lại biểu thức
Đặt:
\(M = \frac{x y + x + 1}{x y + y + 2} = k , k \in \mathbb{Z}\)
Bước 2: Biến đổi biểu thức
Ta có:
\(k \left(\right. x y + y + 2 \left.\right) = x y + x + 1\)
Mở rộng:
\(k x y + k y + 2 k = x y + x + 1\)
Chuyển hết về một phía:
\(k x y - x y + k y - x + 2 k - 1 = 0\)
Nhóm các biến:
\(x y \left(\right. k - 1 \left.\right) + y k - x + \left(\right. 2 k - 1 \left.\right) = 0\)
Bước 3: Xem đây là phương trình theo \(y\)
Nhóm theo \(y\):
\(y \cdot \left[\right. x \left(\right. k - 1 \left.\right) + k \left]\right. = x - \left(\right. 2 k - 1 \left.\right)\)
Nếu \(x \left(\right. k - 1 \left.\right) + k \neq 0\), ta có:
\(y = \frac{x - \left(\right. 2 k - 1 \left.\right)}{x \left(\right. k - 1 \left.\right) + k}\)
Bước 4: Điều kiện \(y\) là số nguyên
Với \(x , k \in \mathbb{Z}\), để \(y\) là số nguyên thì mẫu phải chia hết cho tử.
Bước 5: Trường hợp đặc biệt
Nếu \(x \left(\right. k - 1 \left.\right) + k = 0\), thì:
\(x \left(\right. k - 1 \left.\right) = - k \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } x = \frac{- k}{k - 1}\)
Phải là số nguyên. Ta xét một số giá trị của \(k\) để tìm nghiệm nguyên \(\left(\right. x , y \left.\right)\).
Tóm lại:
Để tìm các cặp \(\left(\right. x , y \left.\right)\), ta có thể thử các giá trị nguyên của \(k\) và \(x\) để tìm \(y\) nguyên.
Bạn muốn mình tiếp tục giải với một số ví dụ cụ thể hoặc bạn cần hướng dẫn giải bằng cách khác không?
Để tìm cặp số nguyên \(\left(\right. x ; y \left.\right)\) sao cho
\(M = \frac{x y + x + 1}{x y + y + 2} = k \in \mathbb{Z}\)
có giá trị nguyên, ta làm cụ thể như sau:
Bước 1: Viết lại
\(k \left(\right. x y + y + 2 \left.\right) = x y + x + 1\)
Mở rộng:
\(k x y + k y + 2 k = x y + x + 1\)
Chuyển về một phía:
\(k x y - x y + k y - x + 2 k - 1 = 0\)
Nhóm:
\(x y \left(\right. k - 1 \left.\right) + y k - x + \left(\right. 2 k - 1 \left.\right) = 0\)
Bước 2: Xét theo \(y\)
\(y \left[\right. x \left(\right. k - 1 \left.\right) + k \left]\right. = x - \left(\right. 2 k - 1 \left.\right)\)
Nếu \(x \left(\right. k - 1 \left.\right) + k \neq 0\), thì
\(y = \frac{x - \left(\right. 2 k - 1 \left.\right)}{x \left(\right. k - 1 \left.\right) + k}\)
Bước 3: Điều kiện \(y \in \mathbb{Z}\)
\(x \left(\right. k - 1 \left.\right) + k \mid x - \left(\right. 2 k - 1 \left.\right)\)
Bước 4: Xét trường hợp mẫu bằng 0
\(x \left(\right. k - 1 \left.\right) + k = 0 \Rightarrow x = \frac{- k}{k - 1}\)
Để \(x \in \mathbb{Z}\), cần \(\left(\right. k - 1 \left.\right) \mid - k\).
Bước 5: Thử các giá trị \(k\)
Trường hợp \(k = 1\):
Vậy với mọi \(x \in \mathbb{Z}\), \(y = x - 1\), thì \(M = 1\).
Trường hợp \(k = 0\):
Muốn \(y \in \mathbb{Z}\), \(\frac{1}{x} \in \mathbb{Z}\) → \(x = \pm 1\).
Trường hợp \(k = 2\):
Muốn \(y \in \mathbb{Z}\), \(x + 2 \mid x - 3\)
\(x - 3 = m \left(\right. x + 2 \left.\right) \Rightarrow x - 3 = m x + 2 m \Rightarrow x - m x = 2 m + 3 \Rightarrow x \left(\right. 1 - m \left.\right) = 2 m + 3\)
Với \(m \in \mathbb{Z}\), \(x = \frac{2 m + 3}{1 - m}\) phải là số nguyên.
Bạn có thể thử các \(m\) để tìm \(x\), sau đó tính \(y\).
Kết luận tóm tắt:
Nếu bạn muốn mình liệt kê thêm cặp \(\left(\right. x , y \left.\right)\) với một số \(k\) cụ thể khác, hãy cho biết nhé!