Hãy chứng minh rằng ba đường phân giác của một tam giác luôn đồng quy tại một điểm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 4 2017
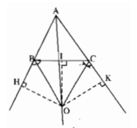
Giả sử hai tia phân giác của các góc ngoài tại đỉnh B và C của tam giác ABC cắt nhau tại O. Ta sẽ chứng minh AO là tia phân giác của góc A.
Kẻ các đường vuông góc OH, OI, OK từ O lần lượt đến các đường thẳng AB, BC, AC.
Vì BO là tia phân giác của góc HBC nên OH = OI (1)
Vì CO là tia phân giác của góc KCB nên OI = OK (2)
Từ (1) và (2) suy ra OI = OH = OK
(3)
Suy ra: O thuộc đường phân giác của góc BAC.
Suy ra AO là tia phân giác của góc BAC và ta có điều phải chứng minh.
LV
8 tháng 8 2021
Gọi I là giao của ∠ABC và ∠ACB, gọi D, F, E lần lượt là hình chiếu của I trên
AC, AB, BC
Xét ∆FBI và ∆EBI:
∠FBI=∠IBE(gt)
BI chung
∠BFI=∠IEB=900(gt) =>∆FBI = ∆EBI(g-c-g)
Do đó IF=IE(cạnh tương ứng)
Xét ∆FAI và ∆DAI:
∠FAI=∠IAD(gt)
AI chung
∠AFI=∠IDA=900(gt) =>∆FAI = ∆DAI(g-c-g)
Do đó IF=ID(cạnh tương ứng)
IF=ID;IF=IE =>ID=IE
Xét ∆ECI và ∆DCI:
∠IEC=∠IDC=900(gt)
ID=IE(CMT)
CI chung => ∆ECI = ∆DCI (cạnh huyền -cạnh góc vuông)
Do đó : ∠ECI=∠ICD
=>IC là phân giác góc BCA
Vậy ba đường phân giác trong CI, AI, BI đồng quy tại một diểm
V
16 tháng 9 2016
Triangle poly1: Polygon A, B, C Segment c: Segment [A, B] of Triangle poly1 Segment a: Segment [B, C] of Triangle poly1 Segment b: Segment [C, A] of Triangle poly1 Segment j: Segment [A, G] Segment k: Segment [B, H] Segment l: Segment [I, C] Segment n: Segment [H, G] Segment q: Segment [O, I] Segment r: Segment [O, G] Segment f_1: Segment [A, D] Segment g_1: Segment [O, K] Segment m: Segment [A, H] Segment p: Segment [B, G] Segment s: Segment [E, D] Segment h_1: Segment [H, O] A = (6.37, 4.19) A = (6.37, 4.19) A = (6.37, 4.19) B = (3.15, -2.53) B = (3.15, -2.53) B = (3.15, -2.53) C = (15.4, -3.36) C = (15.4, -3.36) C = (15.4, -3.36) Point F: Midpoint of c Point F: Midpoint of c Point F: Midpoint of c Point D: Midpoint of a Point D: Midpoint of a Point D: Midpoint of a Point E: Midpoint of b Point E: Midpoint of b Point E: Midpoint of b O = (10.6, -2.67) O = (10.6, -2.67) O = (10.6, -2.67) Point I: Intersection point of f, i Point I: Intersection point of f, i Point I: Intersection point of f, i Point G: Intersection point of d, g Point G: Intersection point of d, g Point G: Intersection point of d, g Point H: Intersection point of e, h Point H: Intersection point of e, h Point H: Intersection point of e, h Point K: Intersection point of j, k Point K: Intersection point of j, k Point K: Intersection point of j, k Point J: Intersection point of f_1, g_1 Point J: Intersection point of f_1, g_1 Point J: Intersection point of f_1, g_1
a) DE là đường trung bình tam giác ABC=>DE//AB và DE=\(\frac{1}{2}\)AB
DE là đường trung bình tam giác OGH=>DE//GH và DE=\(\frac{1}{2}\)GH
=> AB//GH và AB=GH => AHGB là hình bình hành => AG và BH cắt nhau tại trung điểm mỗi đường
CM tương tự: AIGC là hình bình bình hành => AG,IC cắt nhau tại trung điểm mỗi đường
IBCH là hình bình hành => IC,BH cắt nhau tại trung điểm mỗi đường
=> AG,BH,CI đồng quy.
b) K trung điểm AG => OK là trung tuyến tam giác AGO
Mà AD là trung tuyến tam giác AGO ( DG=DO do đối xứng tâm )
=> Giao điểm J của hai đường là trọng tâm tam giác AGO
=> JD =\(\frac{1}{3}\)AD
Mà AD là trung tuyến tam giác ABC
=> J là trọng tâm tam giác ABC
Vậy OK luôn đi qua điểm cố định là trọng tâm tam giác ABC.
CM
3 tháng 5 2019
1). Tam giác ABF và tam giác ACE ần lượt cân tại F, E và
F B A ^ = E C A ^ = A ^ 2 ⇒ Δ A B F ∽ Δ A C E .
2). Giả sử G là giao điểm của BE và CF.
Ta có G F G C = B F C E = A B A C = D B D C ⇒ G D ∥ F B , và F B ∥ A D ta có G ∈ A D .
3). Chứng minh B Q G ^ = Q G A ^ = G A E ^ = G A C ^ + C A E ^ = G A B ^ + B A F ^ = G A F ^ , nên AGQF nội tiếp, và Q P G ^ = G C E ^ = G F Q ^ , suy ra tứ giác FQGP nội tiếp.
26 tháng 1 2024
1) Chứng minh rằng tam giác \( A B F \) đồng dạng với tam giác \( A C E \):
- Tam giác \(ABF\) và \(ACE\) có:
+ Góc \(A\) chung.
+ Góc \(BAF\) bằng góc \(CAE\) (vì \(AD\) là phân giác của góc \(BAC\) và \(CF\), \(BE\) song song với \(AD\)).
Do đó, tam giác \(ABF\) đồng dạng với tam giác \(ACE\) (theo trường hợp góc-góc).
2) Chứng minh rằng các đường thẳng \(BE\), \(CF\), \(AD\) đồng quy:
- Gọi \(G\) là giao điểm của \(BE\) và \(CF\).
- \(AD\) là phân giác góc \(BAC\), và \(BE\), \(CF\) song song với \(AD\). Do đó, \(G\) cũng nằm trên phân giác \(AD\).
- Vậy \(BE\), \(CF\), \(AD\) đồng quy tại \(G\).
3) Chứng minh rằng các điểm \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn:
- Gọi đường tròn ngoại tiếp tam giác \(GEC\) là \(\omega\).
- \(QE\) cắt \(\omega\) tại \(P\) khác \(E\), vậy \(P\) nằm trên đường tròn \(\omega\).
- \(GQ\) song song với \(AE\), và \(AE\) là đường kính của \(\omega\) (vì \(E\) là trung điểm của \(AC\) và \(G\) nằm trên phân giác của \(BAC\)). Do đó, \(GQ\) là dây cung của \(\omega\).
- \(PF\) là tiếp tuyến của \(\omega\) tại \(P\) (vì \(QE\) là tiếp tuyến và \(PF\) là phần kéo dài của \(QE\)).
- Góc \(PGF\) bằng góc \(GAC\) (cùng chắn cung \(GC\) của \(\omega\)).
- \(AF\) là trung trực của \(AB\), nên \(ABF\) là tam giác cân tại \(A\). Do đó, góc \(AFB\) bằng góc \(ABF\).
- Góc \(ABF\) bằng góc \(GAC\) (do đồng dạng của tam giác \(ABF\) và \(ACE\)).
- Vậy, góc \(PGF\) bằng góc \(AFB\). Do đó, \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn.
CM
24 tháng 4 2018
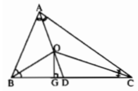
Để chứng minh ∠(BOG) = ∠(COD), ta chứng minh ∠(BOD) = ∠(GOC).
+) Tổng ba góc trong 1 tam giác bằng 180º nên :
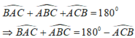
+) Xét tam giác OAB, ta có góc ∠BOD là góc ngoài tam giác tại đỉnh O nên:
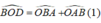
Lại có: BO và AO là tia phân giác của góc B và góc A nên:
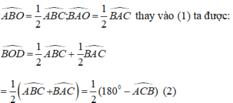
Xét tam giác vuông OCG ta có:
28 tháng 3 2023
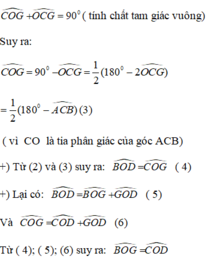
a: ΔABC can tại A
mà AD là trung tuyến
nên AD là phân giác
b: Xet ΔABE và ΔACF có
AB=AC
góc BAE chung
AE=AF
=>ΔABE=ΔACF
=>góc ABE=góc ACF=1/2*góc ABC
=>BE là phân giác của góc ABC
c: Xet ΔABC có
BE,CF,AD là phân giác
=>BE,CF,AD đồng quy
chịu ròi! lớp 1 mà hỏi được câu đấy thì quá ảo !!!!!!
Cho tam giác \(A B C\), chứng minh ba đường phân giác trong của tam giác \(A B C\) đồng quy tại một điểm.
Bước 1: Định nghĩa và ký hiệu
Bước 2: Chứng minh hai đường phân giác đồng quy
Trước tiên, ta chứng minh hai đường phân giác đồng quy tại một điểm, sau đó chứng minh đường phân giác thứ ba cũng đi qua điểm đó.
Chọn hai đường phân giác \(A D\) và \(B E\). Gọi \(I\) là giao điểm của \(A D\) và \(B E\).
Bước 3: Tính chất đường phân giác
Cụ thể:
Bước 4: Vậy \(I\) cách đều các cạnh của tam giác
Từ bước 3, ta thấy \(I\) cách đều \(A B\) và \(A C\) (vì thuộc phân giác góc \(A\)) và cũng cách đều \(B A\) và \(B C\) (vì thuộc phân giác góc \(B\)).
Nhưng \(A B\) và \(B A\) chính là cùng một cạnh, vậy \(I\) cách đều ba cạnh của tam giác \(A B C\).
Bước 5: Đường phân giác thứ ba cũng đi qua \(I\)
Kết luận:
Ba đường phân giác trong tam giác \(A B C\) đồng quy tại điểm \(I\), điểm này còn gọi là trung điểm nội tiếp của tam giác \(A B C\).