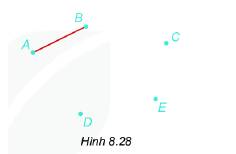
Có 5 hòn đảo biểu thị bởi 5 điểm A,B,C,E
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
6 tháng 10 2023
Đầu mút A: có 4 đoạn thẳng AB, AC, AD, AE.
Đầu mút B: có 3 đoạn thẳng BC, BD, BE (BA trùng với AB nên không đếm).
Đầu mút C: có 2 đoạn thẳng CD, CE (CA trùng AC, CB trùng BC).
Đầu mút D: có 1 đoạn thẳng DE (DA trùng AD, DB trùng BD, DC trùng CD)
Đầu mút E: không thêm đoạn thẳng nào (vì EA trùng AE, EB trùng BE, EC trùng CE, ED trùng DE ở trên).
Do đó cần ít nhất 4 + 3 + 2 + 1 = 10 cây cầu nối hai hòn đảo tùy ý.
Vậy cần phải xây thêm 10 - 1 = 9 cây cầu.
CM
3 tháng 2 2018
Tổng số rồng là 61 : 8 dư 5.
Mỗi lần đấu, số rồng giảm đi 8 nên số rồng còn lại phải chia 8 dư 5.
Đáp án C và E đều đúng (đã thử lại).
CM
18 tháng 2 2017
Tổng số rồng là 61 : 8 dư 5. Mỗi lần đấu, số rồng giảm đi 8 nên số rồng còn lại phải chia 8 dư 5. Đáp án C và E đều đúng (đã thử lại).
CM
23 tháng 11 2019
Đáp án B.
Ta gọi A D = x 0 ≤ x ≤ 50 (km)
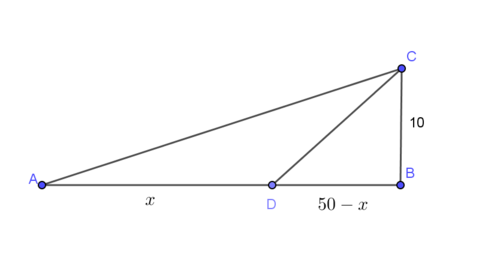
Khi đó: B D = 50 − x ; C D = 100 + 50 − x 2
Từ đó chi phí đi lại là:
f x = 3. x + 5. 100 + 50 − x 2 = 3 x + 5 x 2 − 100 x + 2600
Ta cần tìm để chi phí này là thấp nhất.
Ta có: f ' x = 3 + 5 2 x − 100 2 x 2 − 100 x + 2600 ;
f ' x = 0 ⇔ 6 x 2 − 100 x + 2600 = 500 − 10 x
⇔ x = 42 , 5.
Ta có: f 0 , f 2 < f 42 , 5
Vậy A D = 42 , 5 = 85 2 thì chi phí đi lại là thấp nhất.
24 tháng 7 2016
Áp dụng công thức tính số đường thẳng \(\frac{n.\left(n-1\right)}{2}\)
=> Số đường thẳng tạo được là :
\(\frac{5.\left(5-1\right)}{2}=\frac{5.4}{2}=\frac{20}{2}=10\)( Đường Thẳng)
24 tháng 7 2016
Ta có công thức tính số đường thẳng là : \(\frac{n\left(n-1\right)}{2}\)
Số đường thẳng vẽ được là :
\(\frac{5\left(5-1\right)}{2}=\frac{5\times4}{2}=\frac{20}{2}=10\)đường thẳng
Đáp số : 10 đường thẳng
13 tháng 2 2022
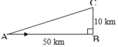
Áp dụng định li Py - ta - go vào △ ABC vuông tại C ta có:
AB2 = BC2 + AC2
AB2 = 122 + 52 = 169
⇒ AB = \(\sqrt{169}=13\)
Vậy cáp treo được xây dựng dài 13 km
ai kết bạn cho 5xu hoặc 49xu