cách tính hình lăng trụ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 9 2023
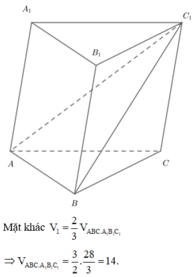
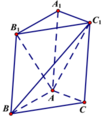
a) Gọi \(I\) là trung điểm của \(BC\).
Tam giác \(ABC\) đều \( \Rightarrow AI \bot BC\)
Tam giác \(A'BC\) cân tại \(A' \Rightarrow A'I \bot BC\)
\( \Rightarrow \left( {\left( {A'BC} \right),\left( {ABC} \right)} \right) = \left( {A'I,AI} \right) = \widehat {AI{\rm{A}}'} = {60^ \circ }\)
Tam giác \(ABC\) đều \( \Rightarrow AI = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)
\( \Rightarrow AA' = AI.\tan \widehat {AI{\rm{A}}'} = \frac{{3a}}{2}\)
b) \({S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\)
\({V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{3{a^3}\sqrt 3 }}{8}\)
CM
27 tháng 4 2018
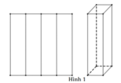
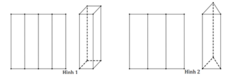
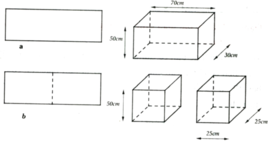
Thể tích thùng tạo ra ở cách 1 là: V1 =50.70.30 = 105000 (cm3).
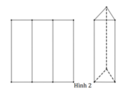
Thể tích hai thùng tạo ra ở cách 2 bằng nhau, thể tích mỗi thùng là: V2 = 50.25.25 = 31250 (cm3)
Vậy các thùng tạo ra ở cách 1 và cách 2 có thể tích không bằng nhau.
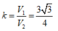
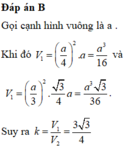
Để tính diện tích và thể tích của hình lăng trụ, ta cần nắm vững một số công thức cơ bản liên quan đến hình lăng trụ. Hình lăng trụ là một hình học không gian có hai mặt đáy là hai đa giác giống nhau và các mặt bên là hình chữ nhật.
1. Diện tích xung quanh (diện tích mặt bên)
Diện tích xung quanh của hình lăng trụ là tổng diện tích các mặt bên của nó. Mỗi mặt bên là một hình chữ nhật có chiều dài bằng cạnh của đa giác đáy và chiều rộng là chiều cao của lăng trụ.
Công thức tính diện tích xung quanh \(S_{\text{xq}}\) của hình lăng trụ là:
\(S_{\text{xq}} = P_{đ \overset{ˊ}{\text{a}} \text{y}} \times h\)
Trong đó:
2. Diện tích toàn phần
Diện tích toàn phần \(S_{\text{tp}}\) của hình lăng trụ là diện tích của tất cả các mặt của nó, bao gồm cả diện tích mặt đáy và diện tích xung quanh.
Công thức tính diện tích toàn phần \(S_{\text{tp}}\) của hình lăng trụ là:
\(S_{\text{tp}} = 2 \times A_{đ \overset{ˊ}{\text{a}} \text{y}} + S_{\text{xq}}\)
Trong đó:
3. Thể tích
Thể tích \(V\) của hình lăng trụ được tính bằng diện tích đáy nhân với chiều cao của lăng trụ.
Công thức tính thể tích \(V\) của hình lăng trụ là:
\(V = A_{đ \overset{ˊ}{\text{a}} \text{y}} \times h\)
Trong đó:
Ví dụ cụ thể:
Giả sử có một hình lăng trụ với đáy là một hình vuông có cạnh dài 4 cm và chiều cao của lăng trụ là 10 cm.
\(A_{đ \overset{ˊ}{\text{a}} \text{y}} = 4^{2} = 16 \textrm{ } \text{cm}^{2}\)
\(P_{đ \overset{ˊ}{\text{a}} \text{y}} = 4 \times 4 = 16 \textrm{ } \text{cm}\)
\(S_{\text{xq}} = P_{đ \overset{ˊ}{\text{a}} \text{y}} \times h = 16 \times 10 = 160 \textrm{ } \text{cm}^{2}\)
\(S_{\text{tp}} = 2 \times A_{đ \overset{ˊ}{\text{a}} \text{y}} + S_{\text{xq}} = 2 \times 16 + 160 = 32 + 160 = 192 \textrm{ } \text{cm}^{2}\)
\(V = A_{đ \overset{ˊ}{\text{a}} \text{y}} \times h = 16 \times 10 = 160 \textrm{ } \text{cm}^{3}\)
Tóm lại:
Hy vọng cách giải này giúp bạn hiểu rõ hơn về cách tính các đại lượng của hình lăng trụ!
bạn làm ở chát jpt