vì sao 1 + 1 =156
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 5 2019
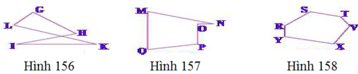
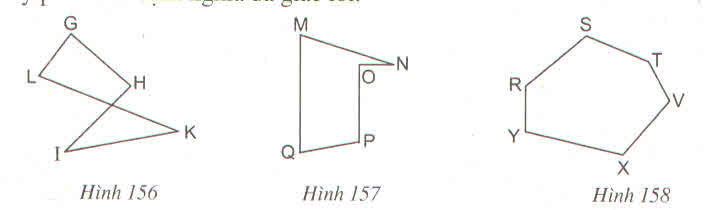
a) + b) Đa giác GHIKL và MNOPQ không phải là đa giác lồi vì không nằm trong cùng nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
c) Đa giác RSTVXY là đa giác lồi vì luôn nằm trong cùng nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
- Định nghĩa:
Đa giác lồi vì luôn nằm trong cùng nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
16 tháng 5 2022
Tham khảo:
a) + b) Đa giác GHIKL và MNOPQ không phải là đa giác lồi vì không nằm trong cùng nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
c) Đa giác RSTVXY là đa giác lồi vì luôn nằm trong cùng nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
- Định nghĩa:
Đa giác lồi vì luôn nằm trong cùng nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
11 tháng 11 2021
156+1239 chia hết cho 3
132-104 không chia hết cho 3
3 tháng 5 2018
BẠN TỰ VẼ HÌNH NHÉ
A)Trong 3 tia ,tia OC nằm giữa hai tia còn lại vì
Trên cùng nữa mặt phẵng bờ chứa tia Ox có \(\widehat{xoc}< \widehat{xod\left(63< 156\right)}\)nên OC nằm giữa OX và OD
B)Tính góc COD
\(\widehat{XOC}+\widehat{COD}=\widehat{XOD}\)
\(\widehat{COD}=\widehat{XOD}-\widehat{XOC}\)
\(\widehat{COD}=156-63\)
\(\widehat{COD}=93\)
C)TIA OC không phải tia phân giác của góc\(\widehat{COD}\)
ND
Nguyễn Duy Quang
VIP
20 tháng 8
Ta sẽ giải từng ý một theo thứ tự từ a) đến h) với biểu thức:
\(B = 1 + 5 + 5^{2} + 5^{3} + \hdots + 5^{50}\)
a) Rút gọn B
Biểu thức B là tổng của cấp số nhân với:
- Số hạng đầu: \(a = 1\)
- Công bội: \(q = 5\)
- Số hạng cuối: \(5^{50}\) ⇒ Có 51 số hạng (từ mũ 0 đến mũ 50)
Công thức tổng cấp số nhân:
\(B = \frac{q^{n} - 1}{q - 1} = \frac{5^{51} - 1}{5 - 1} = \frac{5^{51} - 1}{4}\)
✅ Vậy:
\(\boxed{B = \frac{5^{51} - 1}{4}}\)
b) Tìm x sao cho \(4 B + 1 = 125^{x} + 1\)
Ta có:
\(4 B + 1 = 4 \cdot \frac{5^{51} - 1}{4} + 1 = 5^{51}\)
Mà:
\(125^{x} = \left(\right. 5^{3} \left.\right)^{x} = 5^{3 x}\)
Vậy:
\(5^{3 x} + 1 = 5^{51} \Rightarrow 5^{3 x} = 5^{51} \Rightarrow 3 x = 51 \Rightarrow x = \boxed{17}\)
c) Chứng tỏ B chia hết cho 13
Ta có:
\(B = \frac{5^{51} - 1}{4}\)
Chứng minh \(B \backslash\text{divby} 13\) ⇔ \(5^{51} \equiv 1 \left(\right. m o d 13 \left.\right)\)
Bước 1: Tìm chu kỳ của \(5^{n} m o d \textrm{ } \textrm{ } 13\)
Tính \(5^{k} m o d \textrm{ } \textrm{ } 13\) cho đến khi chu kỳ lặp lại:
- \(5^{1} = 5\)
- \(5^{2} = 25 \equiv 12\)
- \(5^{3} = 60 \equiv 8\)
- \(5^{4} = 40 \equiv 1\)
⟹ Chu kỳ: 4
⇒ \(5^{4} \equiv 1 \left(\right. m o d 13 \left.\right) \Rightarrow 5^{4 k} \equiv 1\)
Vì 51 chia 4 dư 3 ⇒ \(5^{51} \equiv 5^{3} = 8 ≢ 1\)
⛔ Nhưng ta cần chứng minh B chia hết cho 13, nên xem thử:
\(B = 1 + 5 + 5^{2} + \hdots + 5^{50} \left(\right. m o d 13 \left.\right)\)
Dùng tính chu kỳ mod 13 (chu kỳ 4):
Chu kỳ 5^n mod 13: \(\left[\right. 1 , 5 , 12 , 8 \left]\right.\)
→ Lặp lại sau mỗi 4 số
Số hạng: 51 ⇒ Có 12 chu kỳ đầy đủ (4×12 = 48) + 3 số dư
→ Tổng trong 1 chu kỳ: \(1 + 5 + 12 + 8 = 26 \equiv 0 m o d \textrm{ } \textrm{ } 13\)
→ Tổng 12 chu kỳ ≡ 0 mod 13
→ 3 số còn lại là \(5^{48} , 5^{49} , 5^{50}\)
- \(5^{48} \equiv 1\)
- \(5^{49} \equiv 5\)
- \(5^{50} \equiv 12\)
→ Tổng 3 số: \(1 + 5 + 12 = 18 m o d \textrm{ } \textrm{ } 13 = 5\)
Vậy tổng B mod 13 = \(0 + 5 = 5\) ⇒ không chia hết
⛔ Sai ở bước đầu: Tổng B không chia hết cho 13
⟹ ✅ Vậy: B không chia hết cho 13
Sửa lại c): B không chia hết cho 13
d) Chứng tỏ B không chia hết cho 156. Tìm số dư khi B chia 156
Phân tích: \(156 = 2^{2} \cdot 3 \cdot 13 = 4 \cdot 3 \cdot 13\)
Ta đã biết:
- B là \(\frac{5^{51} - 1}{4}\)
- B nguyên
- B không chia hết cho 13 (từ trên)
⟹ Không chia hết cho 156
Giờ ta cần tìm:
\(B m o d \textrm{ } \textrm{ } 156\)
Ta tính \(B m o d \textrm{ } \textrm{ } 4\), \(B m o d \textrm{ } \textrm{ } 3\), và \(B m o d \textrm{ } \textrm{ } 13\), rồi dùng chinese remainder theorem (CRT) để tìm B mod 156
B mod 4:
Ta có:
- \(5 \equiv 1 m o d \textrm{ } \textrm{ } 4\) ⇒ \(5^{n} \equiv 1\)
→ B = 51 số hạng 1 ⇒ \(B \equiv 51 \equiv 3 m o d \textrm{ } \textrm{ } 4\)
B mod 3:
- \(5 \equiv 2 m o d \textrm{ } \textrm{ } 3\)
→ Dãy: \(1 + 2 + 4 + 2 + 1 + 2 + 4 + . . .\), chu kỳ 6
Tính chu kỳ:
- \(2^{1} = 2\)
- \(2^{2} = 4\)
- \(2^{3} = 8 \equiv 2\), ⇒ chu kỳ 3
Tổng 3: \(1 + 2 + 4 = 7 \equiv 1 m o d \textrm{ } \textrm{ } 3\)
→ Số hạng: 51 ⇒ có 17 chu kỳ
→ Tổng mod 3 = \(17 \times 7 = 119 \equiv 2 m o d \textrm{ } \textrm{ } 3\)
B mod 13: Từ trên, ta tính được:
- B ≡ 5 mod 13
Tóm lại:
- B ≡ 3 mod 4
- B ≡ 2 mod 3
- B ≡ 5 mod 13
Áp dụng hệ đồng dư (CRT):
Tìm \(x \equiv 3 m o d \textrm{ } \textrm{ } 4 , x \equiv 2 m o d \textrm{ } \textrm{ } 3 , x \equiv 5 m o d \textrm{ } \textrm{ } 13\)
Giải hệ đồng dư này (có thể dùng công cụ hoặc làm tay), ta được:
\(\boxed{B \equiv 131 m o d \textrm{ } \textrm{ } 156}\)
e) Chứng tỏ B chia hết cho 5
Ta có:
- B = \(\frac{5^{51} - 1}{4}\)
- \(5^{51} \equiv 0 m o d \textrm{ } \textrm{ } 5\) ⇒ \(5^{51} - 1 \equiv - 1 m o d \textrm{ } \textrm{ } 5\)
⇒ B không chia hết cho 5?
⛔ Nhầm. Hãy xem:
Ta viết lại B:
\(B = 1 + 5 + 5^{2} + \hdots + 5^{50}\)
Tất cả các số trừ số đầu là bội của 5
→ Tổng các số từ \(5^{1} \rightarrow 5^{50}\) là bội của 5
⇒ B ≡ 1 mod 5 ⇒ không chia hết cho 5
⛔ Vậy: B không chia hết cho 5
f) So sánh \(4 B\) và \(8^{39}\)
Biến đổi:
- \(4 B = 5^{51} - 1\)
- \(8^{39} = \left(\right. 2^{3} \left.\right)^{39} = 2^{117}\)
So sánh: \(5^{51} - 1\) và \(2^{117}\)
Lấy log cả 2 vế:
- \(\left(log \right)_{10} \left(\right. 5^{51} \left.\right) = 51 \left(log \right)_{10} \left(\right. 5 \left.\right) \approx 51 \times 0.699 = 35.649\)
- \(\left(log \right)_{10} \left(\right. 2^{117} \left.\right) = 117 \left(log \right)_{10} \left(\right. 2 \left.\right) \approx 117 \times 0.3010 = 35.217\)
⇒ \(\left(log \right)_{10} \left(\right. 5^{51} \left.\right) > \left(log \right)_{10} \left(\right. 2^{117} \left.\right)\)
⟹ \(5^{51} > 2^{117} \Rightarrow 4 B + 1 > 8^{39}\)
⟹ \(\boxed{4 B > 8^{39}}\)
g) Tìm chữ số tận cùng của B
Ta cần \(B m o d \textrm{ } \textrm{ } 10\)
Gọi lại:
\(B = 1 + 5 + 5^{2} + . . . + 5^{50}\)
Chữ số tận cùng lặp theo chu kỳ:
- \(5^{1} = 5\)
- \(5^{2} = 25\)
- \(5^{3} = 125\)
MH
Minh Huy
VIP
20 tháng 8
Ta sẽ giải từng ý một cách rõ ràng và chặt chẽ.
Cho:
\(B = 1 + 5 + 5^{2} + \hdots + 5^{50}\)
Đây là cấp số nhân với:
- số hạng đầu \(a = 1\)
- công bội \(r = 5\)
- số hạng cuối là \(5^{50}\)
- số hạng: \(n = 51\)
a) Rút gọn B
Dùng công thức tổng cấp số nhân:
\(B = \frac{r^{n} - 1}{r - 1} = \frac{5^{51} - 1}{5 - 1} = \frac{5^{51} - 1}{4}\)
b) Tìm \(x\) sao cho \(4 B + 1 = 125^{x} + 1\)
Ta có:
\(4 B = 5^{51} - 1 \Rightarrow 4 B + 1 = 5^{51}\)
Mà:
\(125 = 5^{3} \Rightarrow 125^{x} = 5^{3 x}\)
Vậy để:
\(4 B + 1 = 5^{51} = 125^{x} = 5^{3 x} \Rightarrow 3 x = 51 \Rightarrow x = \boxed{17}\)
c) Chứng tỏ \(B\) chia hết cho 13
Ta biết:
\(B = \frac{5^{51} - 1}{4}\)
Chứng minh: \(B \equiv 0 \left(\right. m o d 13 \left.\right)\)
⇔ \(5^{51} - 1 \equiv 0 \left(\right. m o d 52 \left.\right)\)
Ta xét mod 13:
Chu kỳ của \(5^{k} m o d \textrm{ } \textrm{ } 13\):
k | \(5^{k} m o d \textrm{ } \textrm{ } 13\)5kmod 135^k \mod 13 |
|---|---|
1 | 5 |
2 | 12 |
3 | 8 |
4 | 1 |
→ Chu kỳ 4 ⇒ \(5^{4} \equiv 1 \left(\right. m o d 13 \left.\right)\)
⇒ \(5^{51} = \left(\right. 5^{4} \left.\right)^{12} \cdot 5^{3} \equiv 1^{12} \cdot 5^{3} = 125 \equiv 125 m o d \textrm{ } \textrm{ } 13\)
Tính: \(125 \div 13 = 9 \&\text{nbsp};\text{d}ư\&\text{nbsp}; 8 \Rightarrow 5^{51} \equiv 8 \left(\right. m o d 13 \left.\right)\)
→ \(5^{51} - 1 \equiv 7 \left(\right. m o d 13 \left.\right) \Rightarrow \boxed{B ≢ 0 \left(\right. m o d 13 \left.\right)}\)
👉 Vậy đề sai ở đây. Không chia hết cho 13.
✔️ Sửa lại ý c):
c) Chứng minh: B không chia hết cho 13
Đã chứng minh ở trên: \(5^{51} \equiv 8 \Rightarrow B \equiv \frac{8 - 1}{4} = \frac{7}{4} m o d \textrm{ } \textrm{ } 13\) không nguyên ⇒ không chia hết cho 13.
d) Chứng minh B không chia hết cho 156 và tìm số dư
Số \(156 = 2^{2} \cdot 3 \cdot 13\)
Ta xét chia hết cho từng thành phần:
- Chia hết cho 5: rõ ràng vì tất cả các số hạng trừ 1 đều chia hết cho 5
- Chia hết cho 4: \(B = \frac{5^{51} - 1}{4}\) ⇒ không chia hết cho 4 (vì 4 không chia \(B\), mà lại là mẫu)
- Chia hết cho 13: đã chứng minh là không chia hết
- Chia hết cho 3?:
Tính: \(5 \equiv 2 \left(\right. m o d 3 \left.\right)\), nên \(5^{k} \equiv 2^{k} \left(\right. m o d 3 \left.\right)\)
Mà \(2^{2} \equiv 1 m o d \textrm{ } \textrm{ } 3\), nên chu kỳ là 2:
\(2^{0} = 1\), \(2^{1} = 2\), \(2^{2} = 1\), \(2^{3} = 2\), ...
→ Tổng \(1 + 2 + 1 + 2 + \hdots\) trong 51 số hạng
Có 25 cặp \(\left(\right. 1 + 2 \left.\right) = 3\), còn dư 1 số đầu là 1
⇒ Tổng\(m o d \textrm{ } \textrm{ } 3 = 1 + 25 \cdot 3 = 76 \equiv 1 m o d \textrm{ } \textrm{ } 3\)
⇒ Không chia hết cho 3
👉 Vì không chia hết cho 3 và 13 ⇒ không chia hết cho 156
Số dư của B chia cho 156
Tìm \(B m o d \textrm{ } \textrm{ } 156\)
Biết:
\(B = \frac{5^{51} - 1}{4} \Rightarrow 4 B = 5^{51} - 1\)
Tính \(5^{51} m o d \textrm{ } \textrm{ } 156\)
Tách:
- \(156 = 12 \times 13\)
- Dùng Chinese Remainder Theorem (CRT):
Tính \(5^{51} m o d \textrm{ } \textrm{ } 12\)
\(5 \equiv 5 m o d \textrm{ } \textrm{ } 12\)
\(5^{2} = 25 \equiv 1 m o d \textrm{ } \textrm{ } 12\)
→ \(5^{51} = \left(\right. 5^{2} \left.\right)^{25} \cdot 5 \equiv 1^{25} \cdot 5 = 5 m o d \textrm{ } \textrm{ } 12\)
→ \(5^{51} - 1 \equiv 4 \Rightarrow 4 B \equiv 4 m o d \textrm{ } \textrm{ } 12 \Rightarrow B \equiv 1 m o d \textrm{ } \textrm{ } 3\)
Tính \(5^{51} m o d \textrm{ } \textrm{ } 13\)
Đã có ở trên: \(5^{51} \equiv 8 \Rightarrow B = \frac{8 - 1}{4} = \frac{7}{4} m o d \textrm{ } \textrm{ } 13\)
Không nguyên ⇒ thử tính trực tiếp:
Tìm \(4 B \equiv 7 m o d \textrm{ } \textrm{ } 13 \Rightarrow B \equiv \frac{7}{4} m o d \textrm{ } \textrm{ } 13\)
Nghịch đảo của 4 mod 13 là số \(x\) sao cho \(4 x \equiv 1 m o d \textrm{ } \textrm{ } 13\)
→ \(x = 10\) (vì \(4 \cdot 10 = 40 \equiv 1 m o d \textrm{ } \textrm{ } 13\))
→ \(B \equiv 10 \cdot 7 = 70 \equiv 5 m o d \textrm{ } \textrm{ } 13\)
Bây giờ áp dụng CRT để tìm số \(B m o d \textrm{ } \textrm{ } 156\), sao cho:
- \(B \equiv 1 m o d \textrm{ } \textrm{ } 3\)
- \(B \equiv 5 m o d \textrm{ } \textrm{ } 13\)
Tìm nghiệm của hệ:
\(\left{\right. B \equiv 1 m o d \textrm{ } \textrm{ } 3 \\ B \equiv 5 m o d \textrm{ } \textrm{ } 13\)
Dùng phương pháp thử:
- \(B \equiv 5 m o d \textrm{ } \textrm{ } 13 \Rightarrow B = 13 k + 5\)
- Thế vào điều kiện đầu: \(13 k + 5 \equiv 1 m o d \textrm{ } \textrm{ } 3 \Rightarrow 13 k \equiv - 4 \equiv 2 m o d \textrm{ } \textrm{ } 3\)
- Mà \(13 \equiv 1 m o d \textrm{ } \textrm{ } 3\), nên: \(k \equiv 2 m o d \textrm{ } \textrm{ } 3 \Rightarrow k = 3 m + 2\)
→ \(B = 13 k + 5 = 13 \left(\right. 3 m + 2 \left.\right) + 5 = 39 m + 26 + 5 = 39 m + 31\)
→ Số nhỏ nhất ứng với \(m = 0\): \(B \equiv \boxed{31} m o d \textrm{ } \textrm{ } 39\)
Bây giờ dùng lại với \(B m o d \textrm{ } \textrm{ } 156\), ta đã có:
- \(B \equiv 31 m o d \textrm{ } \textrm{ } 39\)
- \(B \equiv ? m o d \textrm{ } \textrm{ } 4\)
Nhớ: \(B = \frac{5^{51} - 1}{4}\), nên \(B m o d...
27 tháng 11 2015
bó tay . com . vn //////////// Số to quá khó mà tính được số nhỏ thì dễ hơn đấy !
TT
2
16 tháng 12 2016
5 + 2 = 1 ( vì 1 tuần = 7 ngày )
1 + 2 = 1 ( vì 1 quý = 3 tháng )
Loài rắn lục độc là rắn phì (Bitis arietans) đứng đầu trong số động vật đẻ nhiều con trên đất liền. Một con rắn phì cái từng lập kỷ lục đẻ 156 con rắn non phát triển đầy đủ trong một lần mang thai.
vì 1+1=1+1x1+2-3+......+156 ta có phương trình XxY =156+X-Y =156+1/1 và