Số tự nhiên n có 6 chữ số phan biệt hai chữ số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số có 6 chữ số phân biệt là \(\overline {abcdef} \).
Chữ số 4 có giá trị bằng 4 000 nên số 4 ở vị trí c. Số cần tìm là \(\overline {ab4def} \)
Vì hai chữ số cạnh nhau luôn là hai số tự nhiên liên tiếp nên số b, 4 và d là 3 số tự nhiên liên tiếp. Do đó, \(\overline {b4d} \) có thể là 345 hoặc 543.
+ Nếu \(\overline {b4d} \) là 345 thì a=2, e=6, f=7. Ta được n = 234 567.
+ Nếu \(\overline {b4d} \) là 543 thì a=6, e=2, f=1. Ta được n = 654 321.
Vậy tìm được 2 số là 234 567 và 654 321.

Câu này mình làm phần bù cho lẹ:
+) số các chữ số phân biệt gồm 6 chữ số là 6.5.8A4=50400 số (bao gồm các TH có số 0,1 và cả trường hợp số 0 đứng đầu)
giải thích: số có 6 chữ số có dáng như abcdef
vây ta có 6 cách xếp số 0
5 cách xếp số 1
và 8A4 cách xếp 4 chữ số còn lại
=> co 50400 số
+) số các chữ số phân biệt gồm 6 chữ số trong đó chỉ có chữ sô 0 đứng đầu (vd: 045381,...) : có 5.8A4=8400 số
giải thích: số 0 đứng đầu nên có 1 cách
số 1 có 5 cách xếp
4 chữ số còn lai có 8A4 cách
Ta dung phần bù: 50400-8400= ......
khong biet dung ko nữa

Chọn C
Số các số tự nhiên có hai chữ số phân biệt là 9.9 = 81 số.
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố “Hai chữ số được viết ra có ít nhất một chữ số chung”
Khi đó ta có biến cố A ¯ là “Hai chữ số được viết ra không có chữ số chung”
Gọi hai chữ số mà Công và Thành viết ra lần lượt là a b ¯ v à c d ¯
- TH1: b = 0, khi đó a có 9 cách, c có 8 cách và d có 7 cách. Vậy có 9.8.7 = 504 cách viết.
- TH2: b ≠ 0, khi đó a có 9 cách, b có 8 cách, c có 7 cách và d có 7 cách. Vậy có 9.8.7.7 = 3528 cách viết.
![]() cách viết.
cách viết.
Vậy xác suất của biến cố A là:
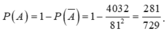
Nhận xét: Đây là một bài toán xác suất chọn số. Đối với bài toán này, ta sẽ đi theo hướng tính gián tiếp thông qua phần bù. Khi đó cách làm sẽ ngắn hơn và tránh nhầm lẫn không đáng có.

Tổng các chữ số của nó là số lẻ khi số chữ số lẻ của nó là lẻ
Các trường hợp thỏa mãn: 1 lẻ 5 chẵn, 3 lẻ 3 chẵn, 5 lẻ 1 chẵn
TH1: 1 lẻ 5 chẵn:
Chọn 1 chữ số lẻ từ 5 chữ số lẻ (1;3;5;7;9) có \(C_5^1\) cách
Chọn 5 chữ số chẵn từ 5 chữ số chẵn (0;2;4;6;8) có \(C_5^5\) cách
Hoán vị 6 chữ số rồi trừ đi trường hợp số 0 đứng đầu: \(6!-5!\) cách
\(\Rightarrow C_5^1.C_5^4.\left(6!-5!\right)=3000\) số
TH2: 3 lẻ 3 chẵn.
Ta có \(C_5^3\) cách chọn 3 chữ số lẻ
Chọn 3 chữ số chẵn bất kì: \(C_5^3\) cách
Hoán vị chúng: \(6!\) cách
\(\Rightarrow C_5^3.C_5^3.6!\) số (tính cả trường hợp 0 đứng đầu)
Chọn 3 chữ số chẵn sao cho có mặt chữ số 0: \(C_4^2\) cách
Hoán vị 6 chữ số sao cho 0 đứng đầu: \(5!\) cách
\(\Rightarrow C_5^3.C_4^2.5!\) cách
\(\Rightarrow C_5^3.C_5^3.6!-C_5^3.C_4^2.5!=64800\) số
TH3: 5 lẻ 1 chẵn
Chọn 5 chữ số lẻ: \(C_5^5=1\) cách
Chọn 1 chữ số chẵn bất kì: 5 cách
Chọn chữ số chẵn sao cho nó là số 0: 1 cách
Hoán vị 6 chữ số 1 cách bất kì: \(6!\) cách
Hoán vị 6 chữ số sao cho số 0 đứng đầu: \(5!\) cách
\(\Rightarrow1.\left(5.6!-1.5!\right)=3480\) số
Cộng 3 TH lại ta có đáp án

Đáp án D
HD: Số cần lập có dạng: a b c d e ¯ ( a , b ; c , d , e ∈ 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 ; a ≠ 0 ) .
THI: Với e = 0 khi đó có 4 cách chọn vị trí cho số 2 và có A 8 3 cách chọn và sắp xếp 3 chữ số còn lại. Do đó có 4 A 8 3 số
TH2: Với e = 2 , khi đó có 3 cách chọn vị trí cho số 0 và có A 8 3 cách chọn và sắp xếp 3 chữ số còn lại. Do đó có 3 A 8 3 số.
TH3: Với e = 4 ; 6 ; 8 , có 3 vị trí sắp xếp số 0, 3 vị trí sắp xếp số 2 và A 7 2 cách chọn và sắp xếp 2 chữ số còn lại. Do đó có 3.3.3. A 7 2 số
Theo quỵ tắc cộng có: 4 A 8 3 + 3 A 8 3 + 27 A 7 2 = 3486 số.

Chọn C
Cách 1: Số các số tự nhiên có hai chữ số phân biệt là 9.9 = 81 số.
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố thỏa mãn bài toán.
+ Khả năng 1: Hai bạn chọn số giống nhau nên có 81 cách.
+ Khả năng 2: Hai bạn chọn số đảo ngược của nhau nên có 9.8 = 72 cách.
+ Khả năng 3: Hai bạn chọn số chỉ có một chữ số trùng nhau
- TH1: Trùng chữ số 0: Công có 9 cách chọn số và Thành đều có 8 cách chọn số nên có 9.8 = 72 cách.
- TH 2: Trùng chữ số 1: Nếu Công chọn số 10 thì Thành có 16 cách chọn số có cùng chữ số 1. Nếu Công chọn số khác 10, khi đó Công có 16 cách chọn số và Thành có 15 cách chọn số có cùng chữ số 1 với Công nên có 16 + 16.15 = 16.16 256 cách.
- Các trường hợp chọn trùng chữ số 2,3,4,....,9 tương tự.
Vậy ![]()
Xác suất cần tính là 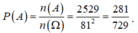
Cách 2: Số các số tự nhiên có hai chữ số phân biệt là 9.9= 81 số.
Số phần tử của không gian mẫu là ![]()
Gọi là biến cố thỏa mãn bài toán. Xét biến cố A ¯
- TH 1: Công chọn số có dạng a 0 ¯ nên có 9 cách. Khi đó có 25 số có ít nhất một chữ số trùng với số a 0 ¯ nên Thành có 81 - 25 = 56 cách chọn số không có chữ số trùng với Công. Vậy có 9.56 = 504 cách.
- TH 2: Công chọn số không có dạng a 0 ¯ : Có 72 cách, khi đó 32 số có ít nhất một chữ số trùng với số của Công chọn nên Thành có 81 - 32 = 49 cách chọn số không có chữ số nào trùng với Thành. Vậy có 72.49 = 3528 cách.
![]()
![]()
Đề bài yêu cầu tìm số tự nhiên \(n\) có 6 chữ số, trong đó tất cả các chữ số là khác nhau, tức là không có chữ số nào lặp lại.
Giải thích:
Cách tính:
Chọn trong 9 chữ số: \(\left{\right. 1 , 2 , . . . , 9 \left.\right}\)
Số cách chọn: 9
Chữ số này khác chữ số hàng nhất và có thể là 0 hoặc các chữ số chưa dùng.
Sau khi đã chọn chữ số hàng nhất, còn lại 9 chữ số (bao gồm 0 nếu chữ số đầu không là 0).
Số cách chọn: 9
Chữ số này khác 2 chữ số đã chọn, còn lại 8 chữ số để chọn.
Số cách: 8
Các chữ số còn lại: 7 chữ số.
Số cách: 7
Các chữ số còn lại: 6 chữ số.
Số cách: 6
Các chữ số còn lại: 5 chữ số.
Số cách: 5
Tổng số số tự nhiên thỏa mãn điều kiện:
\(\boxed{9 \times 9 \times 8 \times 7 \times 6 \times 5}\)Tính:
\(9 \times 9 = 81 81 \times 8 = 648 648 \times 7 = 4536 4536 \times 6 = 27216 27216 \times 5 = 136080\)Vậy, có tổng cộng 136.080 số tự nhiên 6 chữ số, các chữ số khác nhau.