phát biểu định lý thales trong tam giác
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DP
1
Những câu hỏi liên quan
CM
28 tháng 7 2018
Đáp án B
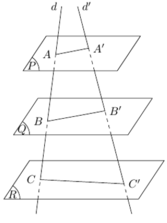
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.
AH
Akai Haruma
Giáo viên
30 tháng 7 2021
Lời giải:
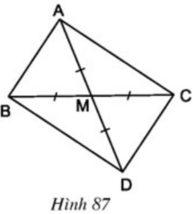
Áp dụng định lý Menelaus cho tam giác $CNB$ có $A,M,D$ thẳng hàng:
$\frac{DC}{DB}.\frac{MN}{MC}.\frac{AB}{AN}=1$
Mà $M$ là trung điểm $CN$ nên $MM=MC$
$\Rightarrow \frac{DC}{DB}.\frac{AB}{AN}=1$
$\Leftrightarrow \frac{AB}{AN}=\frac{DB}{DC}$ (đpcm)
4 tháng 12 2021
b: Tính chất: góc ngoài của tam giác có số đo bằng tổng số đo hai góc trong không kề với nó
a) phát biểu định lý về tổng ba góc một hình tam giác
H
4 tháng 12 2021
a, Trong một tam giác có tổng ba góc của hình tam giác = 180 độ
b, Ta có góc AMB = góc CMD = 40 độ ( đối đỉnh)
Xét tam giác MDC có
góc MDC + góc DCM + góc MCD = 180 ( Định lý tổng ba góc trong tam giác)
=> góc MCD = 180 - góc MDC - góc DCM = 180 - 90 - 40 = 50 độ = x
4 tháng 12 2021
a)3 góc trong tam giác có tổng bằng 180 độ
b)Góc DMC=AMB (2 góc đối đỉnh)
=>DMC=40 độ (Tính chất 2 góc đối đỉnh)
Mà DMC+MDC+x=180 độ (Tổng 3 góc trong tam giác)
=>x=180-DMC-MDC=180-40-90=50 độ
Vậy x=50 độ
9 tháng 5 2022
Refer
Hệ quả của định lí Ta-lét
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh tam giác đã cho.
NG
1
LB
5
3
PG
6 tháng 2 2020
Có trong nâng cao phát triển toán 8 tập 2 nha bạn!!
Ngại viết vì khá là dài :((
6 tháng 2 2020
* Định lí Menelaus: Cho tam giác ABC, một đường thẳng d không đi qua các đỉnh tam giác, cắt các đường thẳng BC,AC,AB lần lượt tại A', B', C'. Khi đó: \(\frac{B'A}{B'C}.\frac{A'C}{A'B}.\frac{C'B}{C'A}=1\)
Cm: Kẻ AH,BK,CN cùng vuông góc với đường thẳng d. Suy ra AH// BK// CN
Theo định lý Ta-lét, ta có: \(\frac{B'A}{B'C}=\frac{AH}{CN};\frac{A'C}{A'B}=\frac{CN}{BK};\frac{C'B}{C'A}=\frac{BK}{AH}\)
Do đó: \(\frac{B'A}{B'C}.\frac{A'C}{A'B}.\frac{C'B}{C'A}=\frac{AH}{CN}.\frac{CN}{BK}.\frac{BK}{AH}=1\)(ĐPCM)
BT
1
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2024
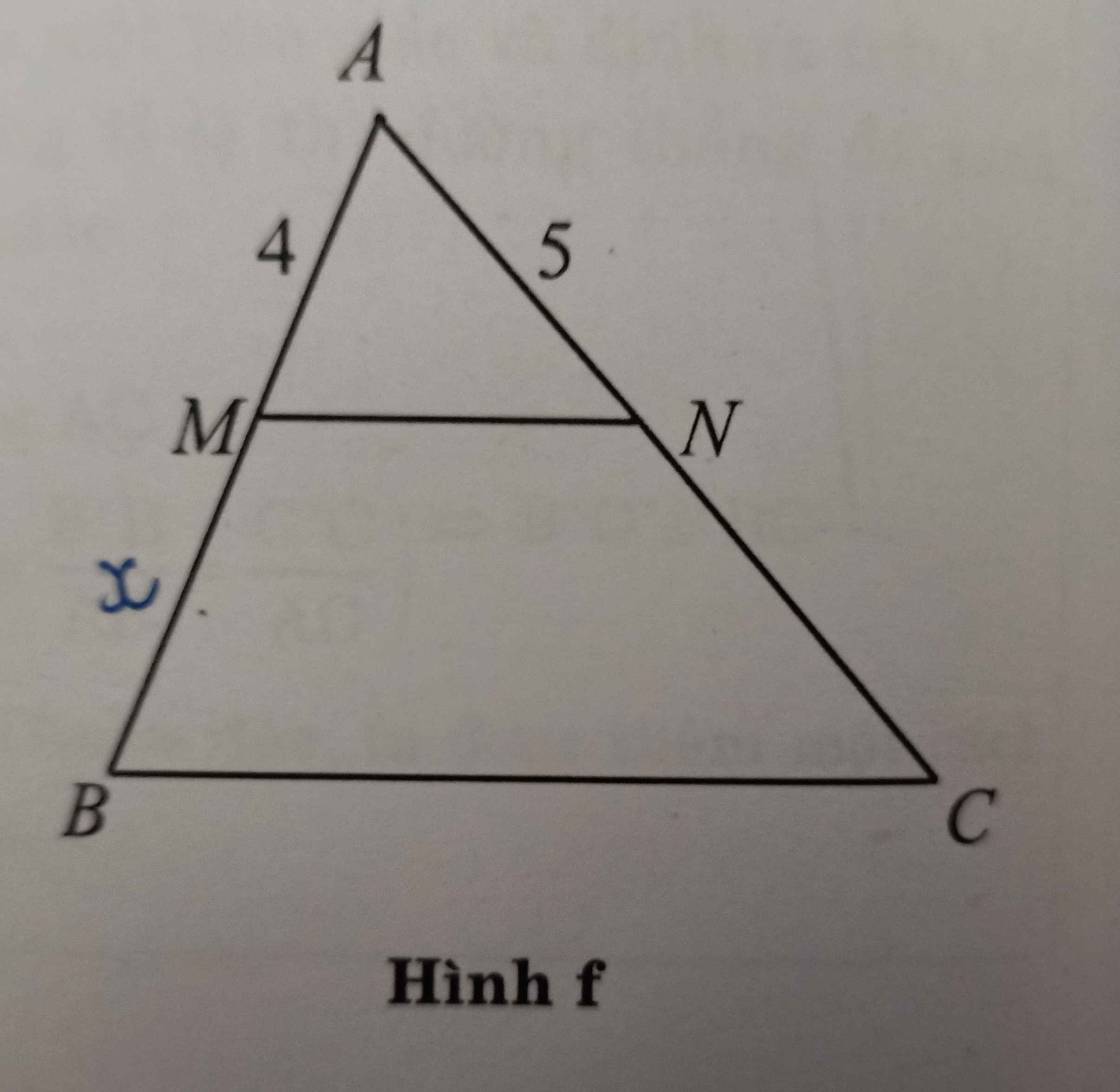
Hình f đề bài thiếu nên không tính được
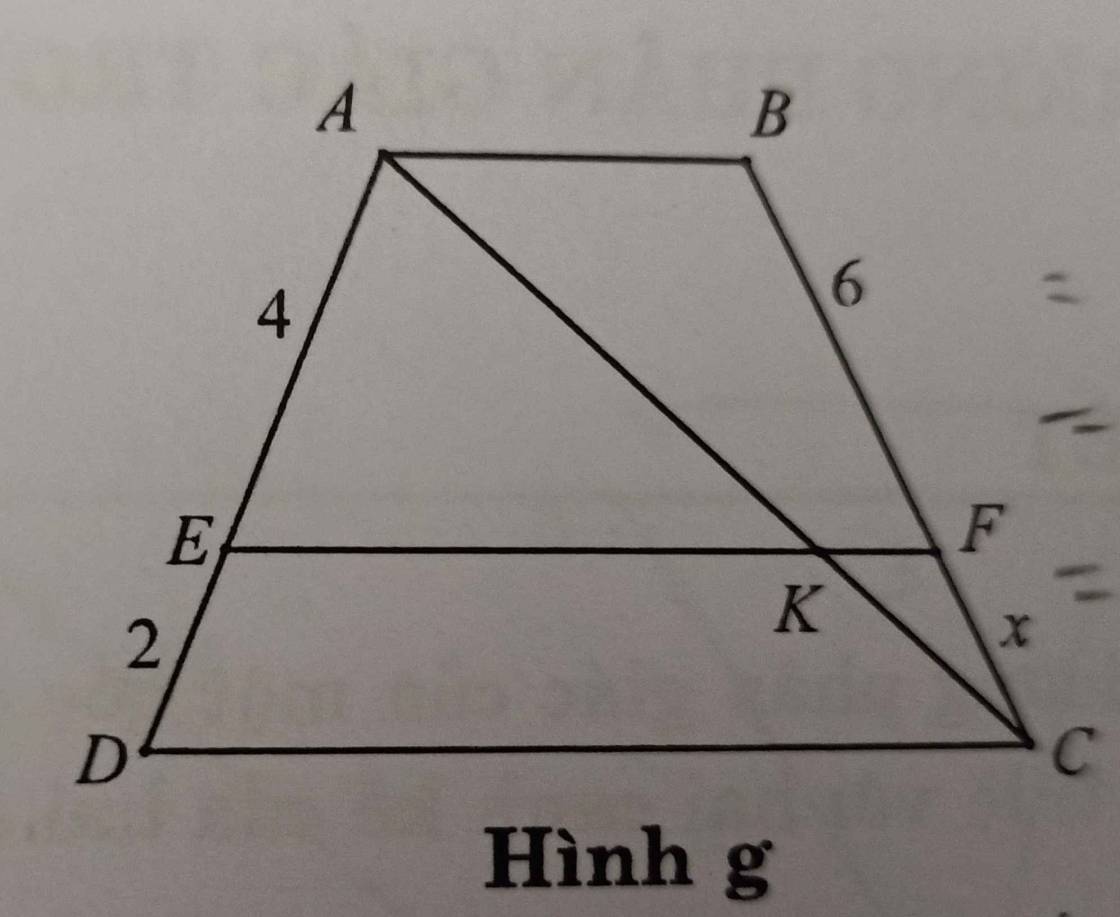
Với hình g:
Áp dụng định lý Talet cho tam giác ADC:
\(\dfrac{AE}{ED}=\dfrac{AK}{KC}\Rightarrow\dfrac{AK}{KC}=\dfrac{4}{2}=2\)
\(\Rightarrow\dfrac{CK}{AK}=\dfrac{1}{2}\)
Áp dụng định lý Talet cho tam giác CAB:
\(\dfrac{CF}{BF}=\dfrac{CK}{AK}\Rightarrow\dfrac{x}{6}=\dfrac{1}{2}\Rightarrow x=3\)
CM
9 tháng 8 2017
a) Tứ giác ABDC có hai đường chéo cắt nhau tại trung điểm mỗi đường ⇒ ABDC là hình bình hành
Hình bình hành ABDC có hai đường chéo bằng nhau ⇒ ABDC là hình chữ nhật
b) ABDC là hình chữ nhật ⇒ góc BAC = 90o
⇒ ΔABC là tam giác vuông tại A
c) Định lí: Tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lai thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.