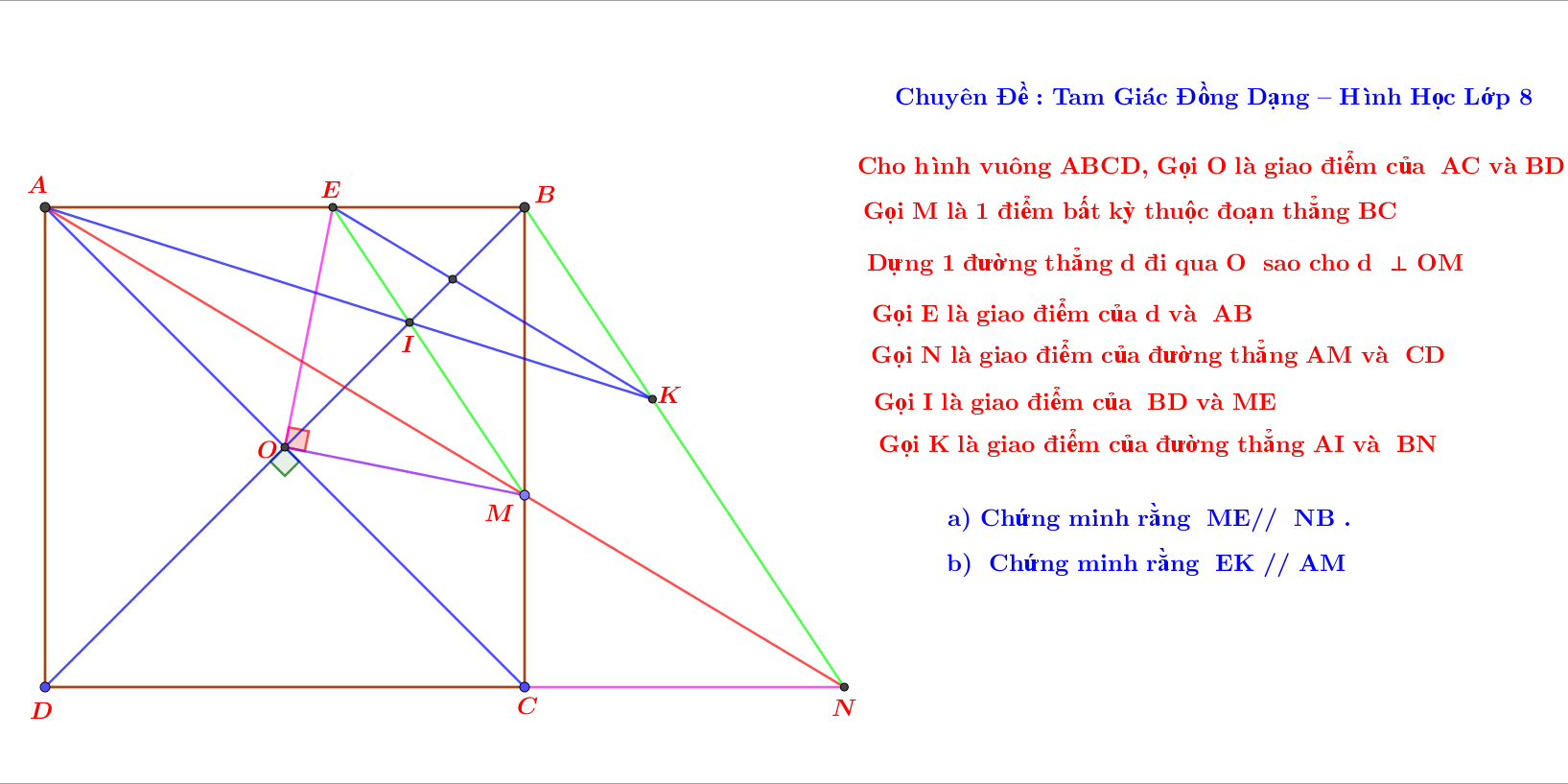
cho hình vuông ABCD có M thuộc BC đường thẳng vuông góc AM tại M cắt CD tại E
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. \(\widehat{AOE}=90^0-\widehat{BOE}=\widehat{BOM}\)
\(\Rightarrow\)△AOE=△BOM (g-c-g). \(\Rightarrow AE=BM;BE=CM\).
△MCN có: CN//AB \(\Rightarrow\dfrac{MN}{AM}=\dfrac{CM}{BM}=\dfrac{BE}{AE}\Rightarrow\)ME//NB.

A F D B E M K C
Có 2 tam giác vuông \(\Delta ABE=\Delta ADF\) vì \(AB=AD\) và \(\widehat{BAE}=\widehat{DAF}\) cùng phụ với \(\widehat{DAE}\)
Suy ra tam giác AEF vuông cân và \(ME=MA=MF\Rightarrow AM\perp EF\)
Ta có \(\overrightarrow{MA}=\left(2;-4\right)\), đường thẳng EF đi qua M có phương trình :
\(2\left(x+4\right)-4\left(y-2\right)=0\Leftrightarrow x-2y+8=0\)
Bây giờ tìm tọa độ các điểm E, F thỏa mãn ME=MA=MF. Gọi T(x;y) thuộc đường thẳng EF, thì x=2t-8; y=t, \(t\in R\)
Khi đó \(MT=MA\Leftrightarrow\left(2t-8+4\right)^2+\left(1-2\right)^2=2^2+\left(-4\right)^2=20\)
\(\Leftrightarrow5\left(t-2\right)^2=20\Leftrightarrow t\left(t-4\right)=0\Leftrightarrow\)\(\begin{cases}t=0\\t=4\end{cases}\)
Như vậy có 2 điểm \(t_1\left(-8;0\right);t_2\left(0;4\right)\) ( Chính là 2 điểm E và F) thuộc đường thẳng EF mà \(MT_1=MA\)
- Trường hợp \(E\left(-8;0\right);F\left(0;4\right)\). Do F thuộc đường thẳng CD nên đường thẳng CD nhận \(\overrightarrow{KF}=\left(3;4\right)\) làm vec tơ chỉ phương.
Phương trình đường thẳng CD là \(\begin{cases}x=3t\\y=4+4t\end{cases}\) (\(t\in R\)).
Khi đó \(D\left(3t;4+4t\right)\)
Ta có \(AD\perp KF\Leftrightarrow\overrightarrow{KF}.\overrightarrow{AD}=0\Rightarrow3\left(3t+6\right)+4\left(-2+4t\right)=0\Leftrightarrow t=-\frac{2}{5}\Rightarrow D\left(-\frac{6}{5};\frac{12}{5}\right)\)
- Trường hợp \(F\left(-8;0\right);E\left(0;4\right)\), đường thẳng CD nhận \(\overrightarrow{FK}=\left(5;0\right)\) làm vec tơ chỉ phương
Phương trình CD : \(\begin{cases}x=-8+5t\\y=0\end{cases}\) \(\left(t\in R\right)\)
Khi đó \(D\left(-8+5t;0\right)\)
Ta có \(AD\perp KF\Leftrightarrow\overrightarrow{FK}.\overrightarrow{AD}=0\Leftrightarrow5\left(-2+5t\right)=0\Leftrightarrow t=\frac{2}{5}\Rightarrow D\left(-6;0\right)\)