Hình tam giác có độ dài đáy là 18cm, chiều cao 8cm. Diện tích hình tam giác đó là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
19 tháng 3 2022
Bài giải
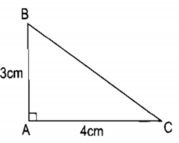
Diện tích hình tam giác đó là :
4 x 3 : 2 = 6 ( cm2 )
Đ/s : 6 cm2 .
CM
27 tháng 1 2018
- Diện tích hình vuông cạnh a: S = a2
- Diện tích tam giác vuông có hai cạnh góc vuông a và b là: S = 0,5 ab
J
16
16 tháng 2 2019
CV=cạnh + cạnh + cạnh
DT=chiều cao nhân đáy tương ứng chia 2
CM
27 tháng 12 2017
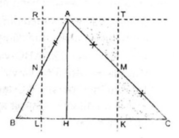
Xét △ ABC. Kẻ đường cao AH. Gọi M là trung điểm của AC, N là trung điểm của AB.
Từ M kẻ đường thẳng song song AH cắt BC tại K
Từ N kẻ đường thẳng song song AH cắt BC tại L
Từ A kẻ đường thẳng song song BC cắt hai đường thẳng MK và NL tại T và R
Ta có: △ MKC = △ MTA
△ NLB = △ NAR
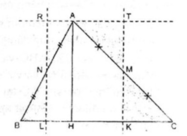
Cắt △ ABC theo đường MK và NL ta ghép lại được một hình chữ nhật KTRL có diện tích bằng diện tích tam giác ABC
24 tháng 3 2018
- Khái niệm chu vi hình bình hành : chu vi của một hình bình hành bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ. Nói cách khác, chu vi hình bình là tổng độ dài của 4 cạnh hình bình hành.
còn hình khác bn tự lm nhé
:3
9 tháng 3 2018
HÌNH CHỮ NHẬT
- Chu vi: P = (a + b) x 2 (P: chu vi)
- Diện tích: S = a x b (S: diện tích)
HÌNH VUÔNG:
- Chu vi: P = a x 4 (P: chu vi)
- Diện tích: S = a x a (S: diện tích)
HÌNH TAM GIÁC:
- Chu vi: P = a + b + c (a: cạnh thứ nhất; b: cạnh thứ hai; c: cạnh thứ ba)
- Diện tích: S = (a x h) : 2 (a: cạnh đáy)
- Chiều cao: h = (S x 2) : a (h: chiều cao)
- Cạnh đáy: a = (S x 2) : h
HÌNH BÌNH HÀNH:
- Chu vi: P = (a + b) x 2 (a: độ dài đáy)
- Diện tích: S = a x h (b: cạnh bên)
- Diện tích: S = a x h (h: chiều cao)
- Độ dài đáy: a = S : h
- Chiều cao: h = S : a
- Diện tích: S = (m x n) : 2 (m: đường chéo thứ nhất)
- Tích 2 đường chéo: (m x n) = S x 2 (n: đường chéo thứ nhất)
- HÌNH THANG
- Diện tích: S = (a + b) x h : 2 (a & b: cạnh đáy)
- Chiều cao: h = (S x 2) : a (h: chiều cao)
- Cạnh đáy: a = (S x 2) : h
HÌNH TRÒN:
- Bán kính hình tròn: r = d : 2 hoặc r = C : 2 : 3,14
- Đường kính hình tròn: d = r x 2 hoặc d = C : 3,14
- Chu vi hình tròn: C = r x 2 x 3,14 hoặc C = d x 3,14
- Diện tích hình tròn: C = r x r x 3,14
- Diện tích xung quanh: Sxq = (a x a) x 4
- Cạnh: (a x a) = Sxq : 4
- Diện tích toàn phần: Stp = (a x a) x 6
- Cạnh: (a x a) = Stp : 6
- Diện tích xung quanh: Sxq = Pđáy x h
- Chu vi đáy: Pđáy = Sxq : h
- Chiều cao: h = Pđáy x Sxq
CM
8 tháng 8 2018
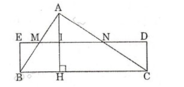
Cho ΔABC với đường cao AH.
Gọi M, N, I là trung điểm của AB, AC, AH.
Lấy E đối xứng với I qua M, D đối xứng với I qua N.
⇒ Hình chữ nhật BEDC là hình cần dựng.
Thật vậy:
Ta có ΔEBM = ΔIAM và ΔDCN = ΔIAN
⇒ SEBM = SAMI và SCND = SAIN
⇒ SABC = SAMI + SAIN + SBMNC = SEBM + SBMNC + SCND = SBCDE.
Suy ra SABC = SBCDE = BE.BC = 1/2.AH.BC. (Vì BE = IA = AH/2).
Ta đã tìm lại công thức tính diện tích tam giác bằng một phương pháp khác
17 tháng 11 2021
\(a,S=\dfrac{1}{2}ah\) (a là cạnh đáy, h là chiều cao)
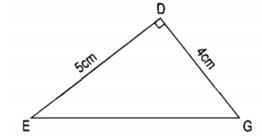
Với tam giác vuông: \(S=\dfrac{1}{2}bc=\dfrac{1}{2}ah\) (b,c là độ dài 2 cạnh góc vuông)
\(b,S_{ABC}=\dfrac{1}{2}AB\cdot AC=300\left(cm^2\right)\)
21 tháng 4 2017
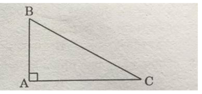
Cho tam giác ABC với đường cao AH. Ta dựng hình chữ nhật có một cạnh bằng một cạnh của tam giác ABC và có diện tích bằng diện tích tam giác ABC như hình dưới
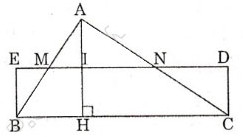
Ta có ∆EBM = ∆KAM và ∆DCN = ∆ KAN
Suy ra
SBCDE = SABC= 
BC. AH
Ta đã tìm được công thức tính diện tích tam giác bằng một phương pháp khác.
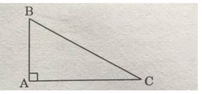
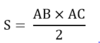
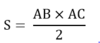
Diện tích tam giác:
18 × 8 : 2 = 72 (cm²)
72