K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 9 2023
1: Xét (O) cso
ME,MF là tiếp tuyến
=>ME=MF
mà OE=OF
nên OM là trung trực của EF
=>OM vuông góc EF tại H và H là trung điểm của EF
2: Xét tứ giác OFAM có
góc OFM=góc OAM=90 độ
=>OFAM nội tiếp
3: Xét ΔOFK và ΔOAF có
góc OFK=góc OAF
góc FOK chung
Do đó: ΔOFK đồng dạng với ΔOAF
=>OF/OA=OK/OF
=>OK*OA=R^2
8 tháng 9 2023
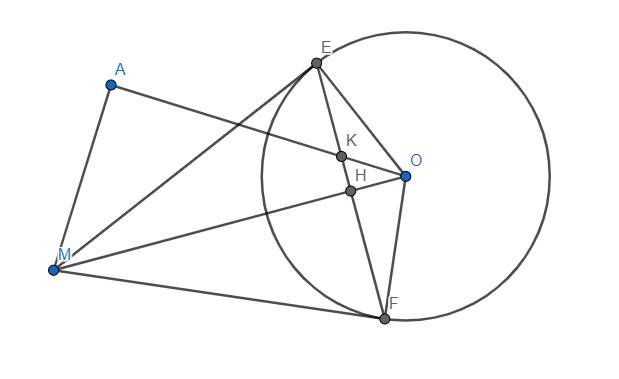
a) Ta thấy \(OE=OF\Rightarrow\) O thuộc trung trực của EF.
Mặt khác, theo tính chất của 2 tiếp tuyến cắt nhau, \(ME=MF\), suy ra M cũng nằm trên trung trực của EF.
\(\Rightarrow\)OM là trung trực của EF. Mà OM cắt EF tại H nên H là trung điểm EF (đpcm)
b) Ta thấy \(\widehat{OAM}+\widehat{OFM}=90^o+90^o=180^o\) nên tứ giác OAMF nội tiếp hay 4 điểm O, M, A, F cùng thuộc 1 đường tròn.
c) Vì OM là trung trực EF nên \(OM\perp EF\) tại H \(\Rightarrow\widehat{MHK}=90^o\)
Từ đó dễ thấy tứ giác AMHK nội tiếp \(\Rightarrow OA.OK=OH.OM\)
Mà \(OH.OM=OE^2=R^2\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow OA.OK=R^2\) (đpcm)
L
23 tháng 1 2022
(C1) tâm I1(0;2) và R1= 3;
(C2) tâm I2( 3;-4) và R2= 3
- Nhận xét :
không cắt C2
- Gọi d: ax+ by+ c= 0 là tiếp tuyến chung , thế thì : d(I1; d) = R1 và d (I2; d) = R2
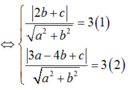
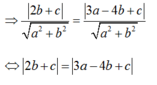
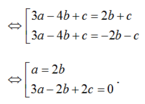
- Trường hợp: a= 2b thay vào (1):
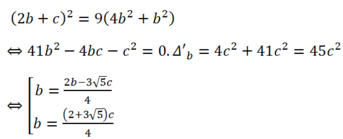
- Do đó ta có hai đường thẳng cần tìm :
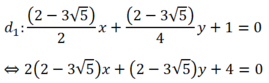
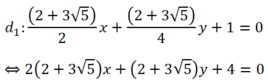
- Trường hợp :
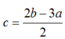
thay vào :
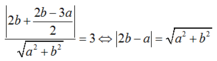
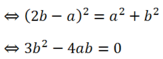
-Có 2 đường thẳng : d3: 2x- 1 = 0 và d4: 6x + 8y -1= 0.
Có tất cả 4 tiếp tuyến chung.
BC
3 tháng 6 2016
chịu thì không lại mất công gõ chư thôi ghi chịu làm gì
10 tháng 1 2023
Xét tứ giác OMAN có
góc OMA+góc ONA=180 độ
nên OMAN là tứ giác nội tiếp
a: Xét (O) có
ΔAKB nội tiếp
AB là đường kính
Do đó: ΔAKB vuông tại K
=>\(\widehat{AKB}=90^0\)
Xét tứ giác NKAH có \(\widehat{NKA}+\widehat{NHA}=90^0+90^0=180^0\)
nên NKAH là tứ giác nội tiếp
=>N,K,A,H cùng thuộc một đường tròn
b: Xét ΔBHN vuông tại H và ΔBKA vuông tại K có
\(\widehat{HBN}\) chung
Do đó: ΔBHN~ΔBKA
=>\(\dfrac{BH}{BK}=\dfrac{BN}{BA}\)
=>\(BH\cdot BA=BN\cdot BK\left(1\right)\)
Xét (O) có
ΔBCA nội tiếp
BA là đường kính
Do đó: ΔBCA vuông tại C
Xét ΔBCA vuông tại C có CH là đường cao
nên \(BH\cdot BA=BC^2\left(2\right)\)
Từ (1),(2) suy ra \(BC^2=BN\cdot BK\)