Cho tam giác QNP,có QN=QP,F thuộc QN;E thuộc QP.QF-QE.NE cắt PF tại H.a)tam giác QEN=QFP và NE=PF b)HN=HP c)góc NQH=góc PQH QH vuông NP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 10 2018
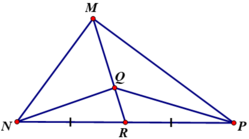
Δ RPQ và Δ RNQ có cùng đường cao.
Gọi m là độ dài đường vuông góc kẻ từ Q đến NP.
30 tháng 4 2023
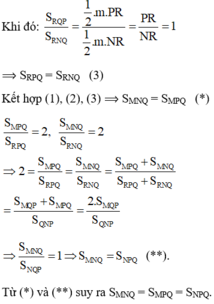
a: Xet ΔAEB và ΔAFC có
góc AEB=góc AFC
góc A chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE/AB=AF/AC
b: Xét ΔAEF và ΔABC co
AE/AB=AF/AC
góc A chung
=>ΔAEF đồng dạng với ΔABC
30 tháng 4 2022
a)
Do \(\triangle ABC \) cân ( \(AB=AC\) )
\(\Rightarrow \widehat{ABC} = \widehat{ACB}\)
Mà \(BE ; CF\) lần lượt là đường phân giác của \(\widehat{ABC} ; \widehat{ACB}.\)
\(\Rightarrow \widehat{ABE} = \widehat{ACF} \)
Xét \(\triangle ABE\) và \(\triangle ACF\) ta có :
\(AB = AC\) ( gt )
\(\widehat{ABC}\) chung
\(\widehat{ABE} = \widehat{ACF} \) ( cmt )
\(\Rightarrow \) \(\triangle ABE\) \(=\) \(\triangle ACF\) ( g.c.g )
6 tháng 2 2022
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường trung trực
hay AH là trục đối xứng của ΔABC
b: Xét ΔABC có
E là trung điểm của AB
M là trung điểm của AC
Do đó: EM là đường trung bình
=>EM//BC và EM=BC/2
hay EM//BH; EM=BH
Xét tứ giác BEMC có ME//BC
nên BEMC là hình thang
mà \(\widehat{EBC}=\widehat{MCB}\)
nên BEMC là hình thang cân
Xét tứ giác BEMH có ME//BH và ME=BH
nên BEMH là hình thang cân
Xét ΔABC có
H là trung điểm của BC
M là trung điểm của AC
Do đó: HM là đường trung bình
=>HM//AB và HM=AB/2
hay HM//AE và HM=AE
=>AEHM là hình bình hành
mà AE=AM
nên AEHM là hình thoi
a: Xét ΔQEN và ΔQFP có
QE=QF
\(\widehat{EQN}\) chung
QN=QP
Do đó: ΔQEN=ΔQFP
=>EN=FP
b: Ta có: QF+FN=QN
QE+EP=QP
mà QF=QE và QN=QP
nên FN=EP
Xét ΔFNP và ΔEPN có
FN=EP
FP=EN
NP chung
Do đó: ΔFNP=ΔEPN
=>\(\widehat{FPN}=\widehat{ENP}\)
=>\(\widehat{HNP}=\widehat{HPN}\)
=>ΔHNP cân tại H
=>HN=HP
c: Xét ΔQNH và ΔQPH có
QN=QP
NH=PH
QH chung
Do đó: ΔQNH=ΔQPH
=>\(\widehat{QNH}=\widehat{QPH}\)
Ta có: QN=QP
=>Q nằm trên đường trung trực của NP(1)
Ta có: HN=HP
=>H nằm trên đường trung trực của NP(2)
Từ (1),(2) suy ra QH là đường trung trực của NP
=>QH\(\perp\)NP