Cách chứng minh vuông góc bằng đường trung trực,trực tâm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
Xét với đường tròn (O) có phương trình \((O):{\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 25\)
Cho các điểm \(A(0;0),B(0;8),C(8;4),D( - 2;4)\) nằm trên đường tròn (O) và thỏa mãn AB vuông góc với CD
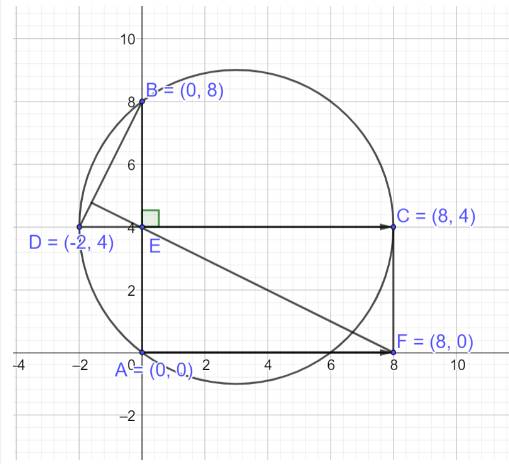
Phương trình đường thẳng đi qua hai điểm A, B có dạng \(x = 0\)
Phương trình đường thẳng đi qua hai điểm C, D có dạng \(y = 4\)
Ta có AB vuông góc với CD tại điểm E nên tọa độ điểm E là nghiệm của hệ sau:
\(\left\{ \begin{array}{l}x = 0\\y = 4\end{array} \right. \Leftrightarrow E(0;4)\)
Gọi tọa độ của điểm F là: \(F(x;y)\)
ACEF là hình chữ nhật nên \(\overrightarrow {AF} = \overrightarrow {EC} \), mặt khác ta có: \(\overrightarrow {AF} = (x;y),\overrightarrow {EC} = \left( {8;0} \right)\)
Suy ra tọa độ điểm F là: \(F\left( {8;0} \right)\)
\(\overrightarrow {EF} = \left( {8; - 4} \right),\overrightarrow {DB} = \left( {2;4} \right) \Rightarrow \overrightarrow {EF} .\overrightarrow {BD} = 8.2 + \left( { - 4} \right).4 = 0 \Rightarrow \overrightarrow {EF} \bot \overrightarrow {BD} \)
Vậy ta chứng minh được EF vuông góc với DB
19 tháng 7 2017
Tứ giác ABCD có AC vuông góc BD và AC cắt BD tạo O
\(AB^2=0A^2+OB^2\)
\(CD^2=OC^2+OD^2\)
\(AD^2=OA^2+OD^2\)
\(BC^2=OB^2+OC^2\)
\(\Rightarrow AB^2+CD^2=OA^2+OB^2+OC^2+OD^2\)(1)
\(AD^2+BC^2=OA^2+OD^2+OB^2+OC^2\)(2)
Từ (1) và 92) \(\Rightarrow AB^2+CD^2=AD^2+BC^2\)
NX
3 tháng 9 2016
Gọi giao của AC và BD là O , do hai đường chéo vuông góc
=> các tam giác : OAB, OBC, OCD, ODA là các tam giác vuông tại O
xét tam giác OAB có AB^2 = OA^2 + OB^2 (1)
xét tam giác ODC có DC^2 = OD^2 + OC^2 (2)
xét tam giác OAD có AD^2 = OA^2 + OD^2 (3)
xét tam giác OBC có BC^2 = OC^2 + OB^2 (4)
từ (1) và (2)=> AB^2 + CD^2 = OA^2 +OB^2 +OC^2 +OD^2 (5)
từ (3) và (4)=> BC^2 + AD^2 = OA^2 +OB^2 +OC^2 +OD^2 (6)
từ (5) và (6) => AB^2 + CD^2 = BC^2 + AD^2 ( dpcm )
Mình làm đúng không các bạn ??? Đúng thì nha !!
Để chứng minh vuông góc bằng đường trung trực và trực tâm, bạn có thể áp dụng các định nghĩa, tính chất và phương pháp sau đây:
1.Chứng minh vuông góc bằng đường trung trực
Định nghĩa đường trung trực
Cách chứng minh một đường thẳng là đường trung trực
Từ đó suy ra
Ví dụ minh họa
Cho tam giác cân \(\triangle A B C\) với \(A C = B C\). Gọi \(I\) là trung điểm của \(A B\). Chứng minh đường thẳng \(C I\) là đường trung trực của \(A B\).
Giải:
2.Chứng minh vuông góc bằng trực tâm
Định nghĩa trực tâm
Cách chứng minh
Ví dụ minh họa
Cho tam giác \(\triangle A B C\), gọi \(H\) là giao điểm của hai đường cao \(A D\) và \(B E\) (với \(D \in B C\), \(E \in A C\)).
Chứng minh: \(C H\) cũng vuông góc với \(A B\).
Giải:
Tóm tắt
Phương pháp
Cách chứng minh vuông góc
Ví dụ minh họa
Đường trung trực
Chứng minh đường thẳng vuông góc tại trung điểm đoạn thẳng
Đường trung trực trong tam giác cân
Trực tâm
Chứng minh giao điểm của hai đường cao, đường cao thứ ba vuông góc với cạnh đối diện
Giao điểm ba đường cao trong tam giác
Nếu bạn cần bài tập cụ thể hoặc hướng dẫn chi tiết hơn, mình có thể hỗ trợ thêm nhé!