K
Khách
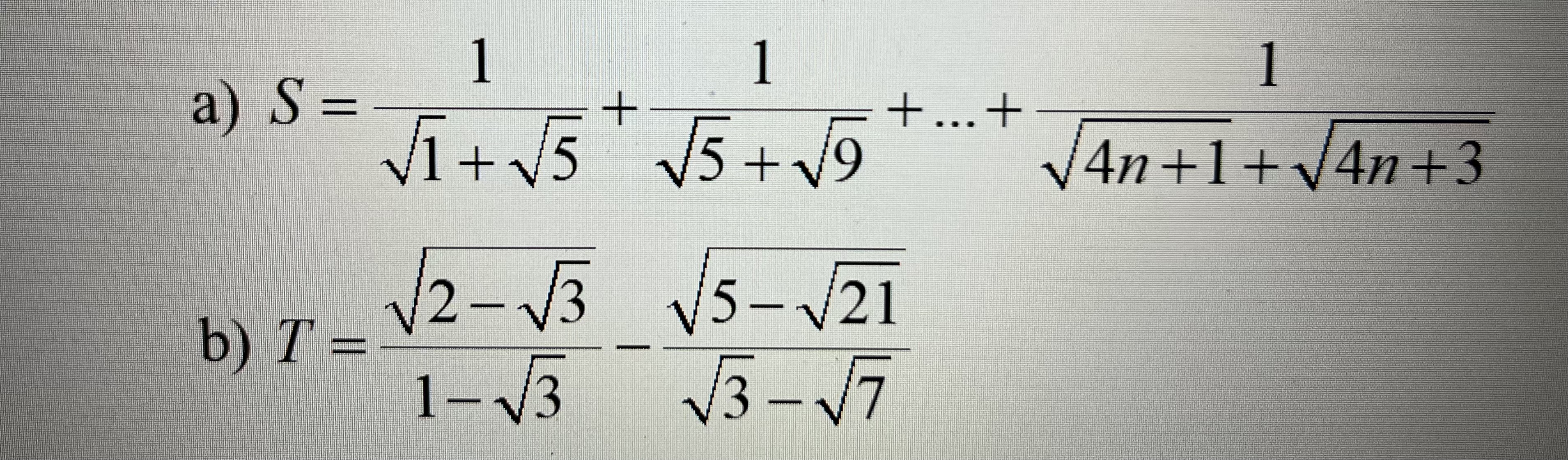
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
B
1
12 tháng 9 2021
Ta có: \(\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}+\sqrt{\left(2-\sqrt{5}\right)^2}-2\sqrt{5}\)
\(=\sqrt{5}+\sqrt{5}-2-2\sqrt{5}\)
=-2
NL
2
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
26 tháng 1 2021
\(\frac{1515}{2525}=\frac{15x101}{25x101}=\frac{3}{5}\)
10 tháng 11 2021
Tham khảo:
Điều kiện xác định của phương trình là tập hợp các giá trị của ẩn làm cho tất cả các mẫu trong phương trình đều khác 0. Điều kiện xác định của phương trình viết tắt là ĐKXĐ.
20 tháng 1 2022
\(=\sqrt{5}-\sqrt{3}+\sqrt{5}-2=2\sqrt{5}-2-\sqrt{3}\)
8 tháng 9 2021
\(e,\left(5+2\sqrt{6}\right)\left(49-20\sqrt{6}\right)\sqrt{5-2\sqrt{6}}\\ =\left(5+2\sqrt{6}\right)\left(\sqrt{3}-\sqrt{2}\right)\left(5-2\sqrt{6}\right)^2\\ =\left(5-2\sqrt{6}\right)\left(\sqrt{3}-\sqrt{2}\right)\\ =\left(\sqrt{3}-\sqrt{2}\right)^2\left(\sqrt{3}-\sqrt{2}\right)=\left(\sqrt{3}-\sqrt{2}\right)^3\)
\(f,\left(2\sqrt{6}-4\sqrt{3}+5\sqrt{2}-\dfrac{1}{4}\sqrt{8}\right)\cdot3\sqrt{6}\\ =36-36\sqrt{2}+30\sqrt{3}-3\sqrt{3}=36-36\sqrt{2}+27\sqrt{3}\)
\(g,\left(2+\sqrt{3}-\sqrt{2}\right)\left(2-\sqrt{3}-\sqrt{2}\right)\left(3+\sqrt{2}\right)\sqrt{3-2\sqrt{2}}\\ =\left[\left(2-\sqrt{2}\right)^2-\left(\sqrt{3}\right)^2\right]\left(3+\sqrt{2}\right)\sqrt{\left(\sqrt{2}-1\right)^2}\\ =\left(3-4\sqrt{2}\right)\left(3+\sqrt{2}\right)\left(\sqrt{2}-1\right)\\ =\left(1-9\sqrt{2}\right)\left(\sqrt{2}-1\right)\\ =10\sqrt{2}-37\)
\(h,A=\sqrt{4+\sqrt{10+2\sqrt{5}}}+\sqrt{4-\sqrt{10+2\sqrt{5}}}\\ A^2=4+\sqrt{10+2\sqrt{5}}+4-\sqrt{10+2\sqrt{5}}+2\sqrt{\left(4+\sqrt{10+2\sqrt{5}}\right)\left(4-\sqrt{10+2\sqrt{5}}\right)}\\ A^2=8+2\sqrt{6-2\sqrt{5}}\\ A^2=8+2\left(\sqrt{5}-1\right)\\ A^2=6+2\sqrt{5}\\ A=\sqrt{6+2\sqrt{5}}=\sqrt{\left(\sqrt{5}+1\right)^2}=\sqrt{5}+1\)
8 tháng 9 2021
\(b,\sqrt{15-\sqrt{216}}+\sqrt{33-12\sqrt{6}}\\ =\sqrt{15-6\sqrt{6}}+\sqrt{\left(2\sqrt{6}-3\right)^2}\\ =\sqrt{\left(3-\sqrt{6}\right)^2}+2\sqrt{6}-3\\ =3-\sqrt{6}+2\sqrt{6}-3=\sqrt{6}\)
\(c,\sqrt{2-\sqrt{3}}\left(\sqrt{6}+\sqrt{2}\right)\\ =\sqrt{12-6\sqrt{3}}+\sqrt{4-2\sqrt{3}}\\ =\sqrt{\left(3-\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{3}-1\right)^2}\\ =3-\sqrt{3}+\sqrt{3}-1=2\)
8 tháng 9 2021
c: \(\sqrt{2-\sqrt{3}}\cdot\left(\sqrt{6}+\sqrt{2}\right)\)
\(=\sqrt{4-2\sqrt{3}}\cdot\left(\sqrt{3}+1\right)\)
\(=\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)\)
=3-1
=2
HT
2
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 1 2024
\(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
\(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(b+1\right)}=\dfrac{b}{a}\)
T
12 tháng 1 2024
d) Để phân thức \(\dfrac{4x^3+4x^2}{x^2-1}\) có nghĩa thì: \(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
Khi đó: \(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
e) Để phân thức \(\dfrac{b^2+b}{a+ab}\) có nghĩa thì: \(a+ab\ne0\Leftrightarrow a\ne-ab\)
Khi đó: \(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(1+b\right)}=\dfrac{b}{a}\)
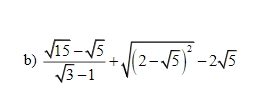
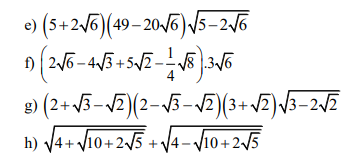
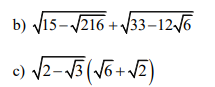
a: Sửa đề: \(S=\dfrac{1}{\sqrt{1}+\sqrt{5}}+\dfrac{1}{\sqrt{5}+\sqrt{9}}+...+\dfrac{1}{\sqrt{4n-3}+\sqrt{4n+1}}\)
\(=\dfrac{-\sqrt{1}+\sqrt{5}}{4}+\dfrac{-\sqrt{5}+\sqrt{9}}{4}+...+\dfrac{-\sqrt[]{4n-3}+\sqrt{4n+1}}{4}\)
\(=\dfrac{-\sqrt{1}+\sqrt{5}-\sqrt{5}+\sqrt{9}-...-\sqrt{4n-3}+\sqrt{4n+1}}{4}=\dfrac{\sqrt{4n+1}-1}{4}\)
b: \(T=\dfrac{\sqrt{2-\sqrt{3}}}{1-\sqrt{3}}-\dfrac{\sqrt{5-\sqrt{21}}}{\sqrt{3}-\sqrt{7}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\dfrac{\sqrt{4-2\sqrt{3}}}{1-\sqrt{3}}-\dfrac{\sqrt{10-2\sqrt{21}}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\cdot\left(\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{1-\sqrt{3}}-\dfrac{\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\cdot\left(\dfrac{\sqrt{3}-1}{1-\sqrt[]{3}}-\dfrac{\sqrt{7}-\sqrt{3}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(-1+\dfrac{\sqrt{7}-\sqrt{3}}{\sqrt{7}-\sqrt{3}}\right)=0\)