Question

[Gia Bảo]

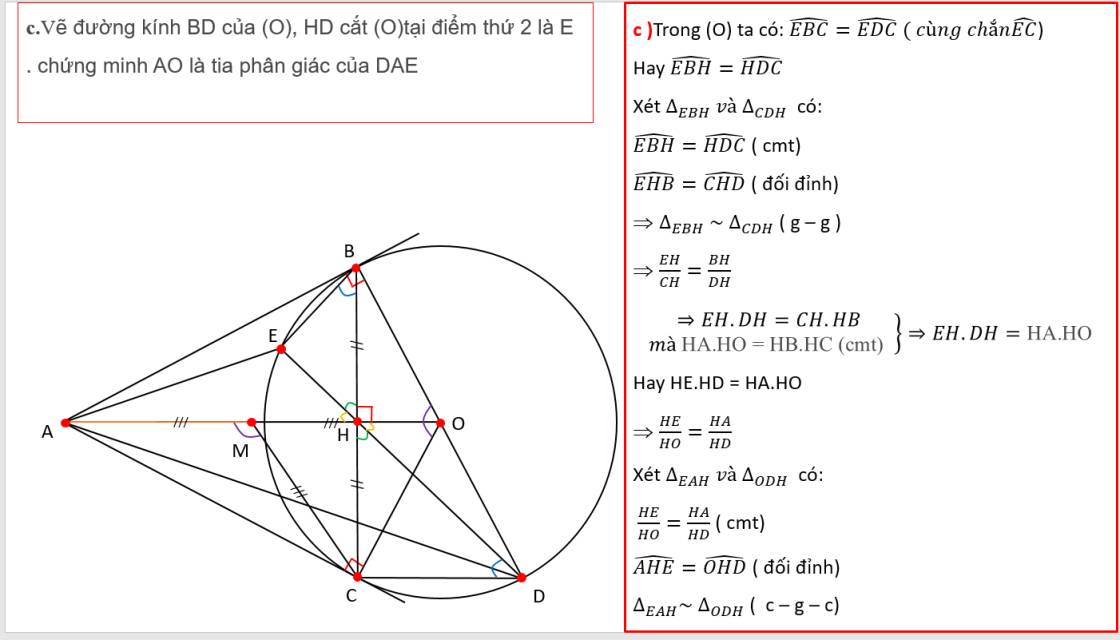
Từ điểm A nằm ngoài đường tròn (O;R) kẻ hai tiếp tuyển AB , AC với đường tròn đó (tại các tiếp điểm B và C) a) chứng minh tứ giác ABOC nội tiếp đường tròn B) vẽ đường kính BD của (O) .chứng minh OA//CD C) đường thẳng đi qua điểm I vuông góc với AD cắt đường thẳng BC tại điểm E . Chứng minh ED là tiếp tuyến của (O)

Answer 1

[Nguyễn Lê Phước Thịnh]

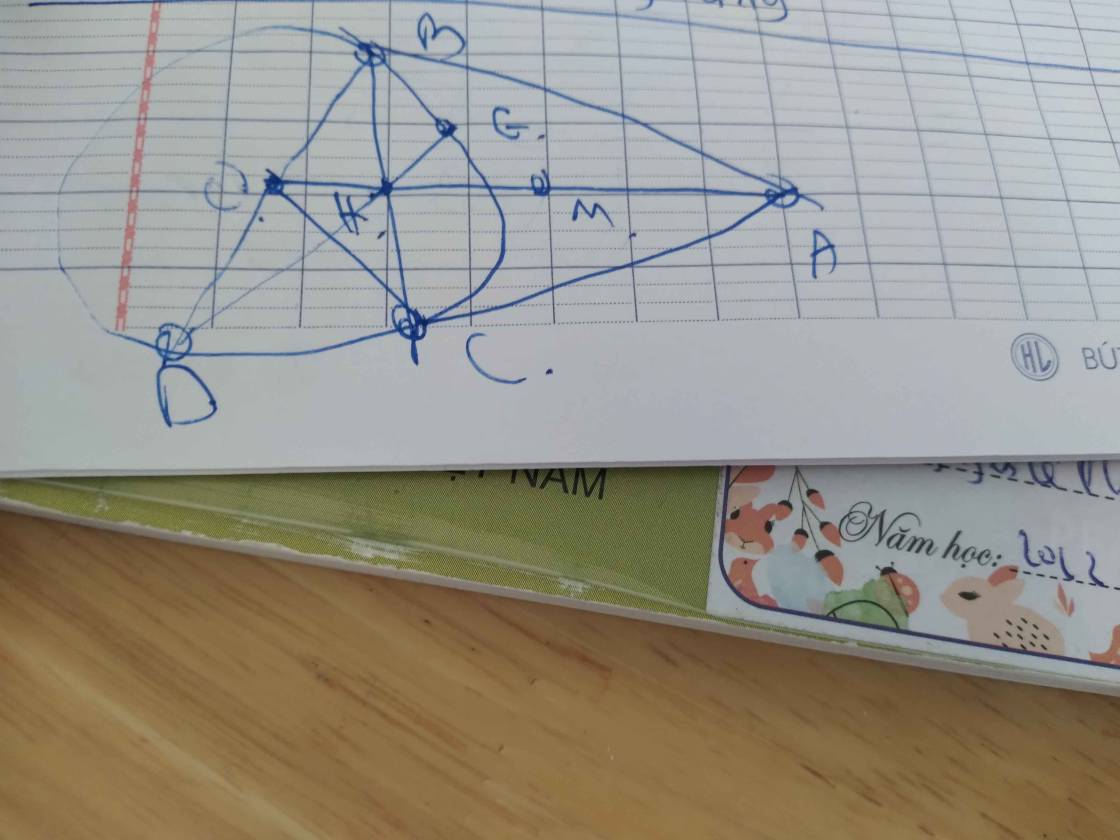
a: Xét tứ giác OBAC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)

nên OBAC là tứ giác nội tiếp

b: Xét (O) có

AB,AC là các tiếp tuyến

Do đó: AB=AC

=>A nằm trên đường trung trực của BC(3)

Ta có: OB=OC

=>O nằm trên đường trung trực của BC(4)

Từ (3),(4) suy ra OA là đường trung trực của BC

=>OA\(\perp\)BC

Xét (O) có

ΔBCD nội tiếp

BD là đường kính

Do đó: ΔBCD vuông tại C

=>BC\(\perp\)CD

mà OA\(\perp\)BC

nên OA//CD

c: Sửa đề: Đường thẳng qua O vuông góc với AD cắt BC tại E

Gọi H là giao điểm của BC và OA

Vì OA là đường trung trực của BC

nên OA\(\perp\)BC tại H và H là trung điểm của BC

Gọi I là giao điểm của OE và DA

Theo đề, ta có: OE\(\perp\)DA tại I

Xét ΔOIA vuông tại I và ΔOHE vuông tại H có

\(\widehat{IOA}\) chung

Do đó: ΔOIA~ΔOHE

=>\(\dfrac{OI}{OH}=\dfrac{OA}{OE}\)

=>\(OI\cdot OE=OH\cdot OA\left(1\right)\)

Xét ΔOBA vuông tại B có BH là đường cao

nên \(OH\cdot OA=OB^2=R^2\left(2\right)\)

Từ (1),(2) suy ra \(OI\cdot OE=R^2=OD^2\)

=>\(\dfrac{OI}{OD}=\dfrac{OD}{OE}\)

Xét ΔOID và ΔODE có

\(\dfrac{OI}{OD}=\dfrac{OD}{OE}\)

\(\widehat{IOD}\) chung

Do đó: ΔOID~ΔODE

=>\(\widehat{OID}=\widehat{ODE}\)

=>\(\widehat{ODE}=90^0\)

=>DE là tiếp tuyến của (O)