 giúp tớ vs ạ , tớ đang cần gấp ạ
giúp tớ vs ạ , tớ đang cần gấp ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NM
2

Những câu hỏi liên quan

TM
1


14 tháng 3 2022
Tớ ko giúp đc)): cọu tự tra google đuy,chứ có google để làm j ((:?
PN
1

11 tháng 12 2021
Bài 1:
b: Xét ΔOAC và ΔOBD có
OA=OB
\(\widehat{AOC}=\widehat{BOD}\)
OC=OD
Do đó: ΔOAC=ΔOBD
PN
11 tháng 12 2021
Nếu cậu làm hết thì tớ sẽ thả đúng và một lượt theo dõi:3(không làm cũng không sao tớ cảm ơn)
TL
0

PN
0






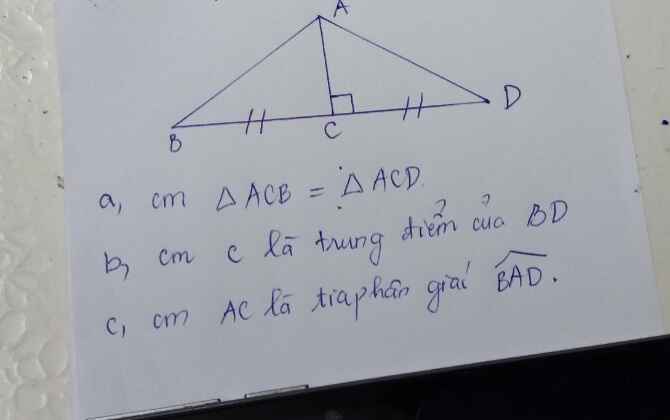 giúp tớ với, tớ đang cần gấp ạ.
giúp tớ với, tớ đang cần gấp ạ.
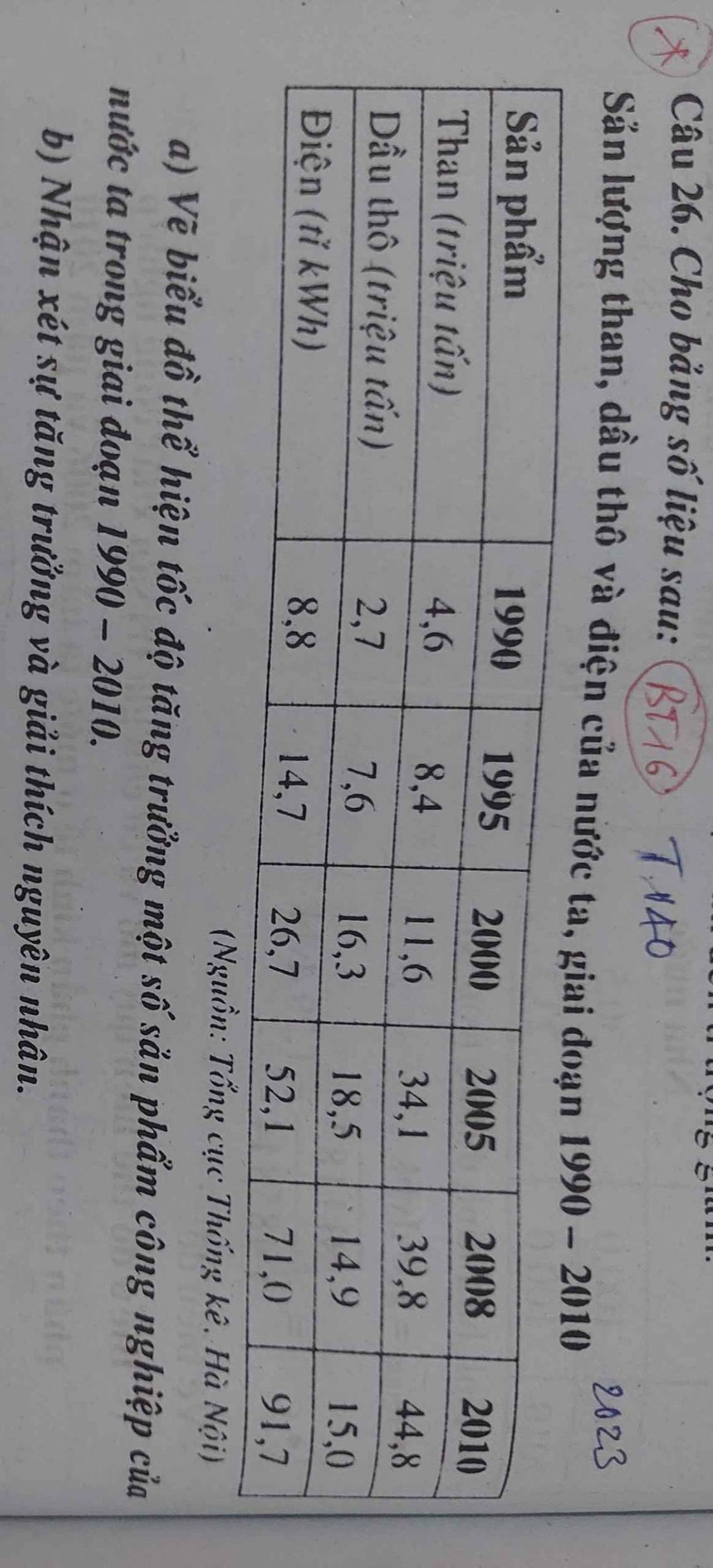
 giúp tớ bài này với ạ:3 tớ đang cần gấp
giúp tớ bài này với ạ:3 tớ đang cần gấp



a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
Do đó: ΔOAB~ΔOCD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
=>\(\dfrac{OA}{OC+OA}=\dfrac{OB}{OD+OB}\)
=>\(\dfrac{AO}{AC}=\dfrac{BO}{BD}\)(2)
Xét ΔADC có OM//DC
nên \(\dfrac{OM}{DC}=\dfrac{AO}{AC}\left(1\right)\)
Xét ΔBDC có ON//DC
nên \(\dfrac{ON}{DC}=\dfrac{BO}{BD}\left(3\right)\)
Từ (1),(2),(3) suy ra OM=ON
b: Xét ΔADC có OM//DC
nên \(\dfrac{OM}{DC}=\dfrac{AO}{AC}\)
Xét ΔCAB có ON//AB
nên \(\dfrac{ON}{AB}=\dfrac{CO}{CA}\)
\(\dfrac{OM}{DC}+\dfrac{ON}{AB}=\dfrac{AO}{AC}+\dfrac{CO}{AC}=\dfrac{AO+CO}{AC}=\dfrac{AC}{AC}=1\)
=>\(OM\left(\dfrac{1}{AB}+\dfrac{1}{CD}\right)=1\)
=>\(\dfrac{1}{AB}+\dfrac{1}{CD}=\dfrac{1}{OM}=\dfrac{2}{MN}\)
Đề bài tóm tắt:
Cho hình thang \(A B C D\) với \(A B \parallel C D\), hai đường chéo \(A C\) và \(B D\) cắt nhau tại \(O\).
Kẻ đường thẳng qua \(O\), song song với hai đáy \(A B\) và \(C D\), cắt \(A D\) tại \(M\), và cắt \(B C\) tại \(N\).
a) Chứng minh \(O M = O N\)
Lý do:
Ta có:
Hoặc đơn giản hơn:
Tam giác đồng dạng + đường song song → đoạn thẳng OM = ON
=> Kết luận: \(O M = O N\)
b) Chứng minh:
\(\frac{1}{A B} + \frac{1}{C D} = \frac{2}{M N}\)
Lý do:
Dùng tính chất đường trung bình trong tam giác + biến đổi tỉ lệ:
→ Có công thức chuẩn:
\(\frac{1}{A B} + \frac{1}{C D} = \frac{2}{M N}\)
Đây là định lý hình học kinh điển, có thể chứng minh bằng tam giác đồng dạng hoặc biến đổi tỉ số đoạn thẳng theo hệ số đồng dạng.
c) Biết:
Tính diện tích tứ giác \(A B C D\):
Phân tích:
Hai tam giác tạo thành hình thang là:
\(S_{A B C D} = S_{A O B} + S_{C O D} = 2008^{2} + 2009^{2}\)
Tính toán:
Áp dụng hằng đẳng thức:
\(a^{2} + b^{2} = \left(\right. a + b \left.\right)^{2} - 2 a b\)
Ta có:
\(S_{A B C D} = 2008^{2} + 2009^{2} = \left(\right. 2008 + 2009 \left.\right)^{2} - 2 \cdot 2008 \cdot 2009\) \(= 4017^{2} - 2 \cdot 2008 \cdot 2009\)
Tính chi tiết:
Tính:
\(2008 \cdot 2009 = \left(\right. 2008 \left.\right) \left(\right. 2008 + 1 \left.\right) = 2008^{2} + 2008 = 4 , 032 , 064 + 2008 = 4 , 034 , 072\) \(\Rightarrow 2 \cdot 2008 \cdot 2009 = 2 \cdot 4 , 034 , 072 = 8 , 068 , 144\)
Cuối cùng:
\(S_{A B C D} = 16 , 136 , 289 - 8 , 068 , 144 = \boxed{8 , 068 , 145}\)
✅ Đáp án: