Giải phương trình : 2sinx+cscx=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


8cos2x + 2sinx – 7 = 0 (1)
⇔ 8(1 – sin2x) + 2sinx – 7 = 0
⇔ 8sin2x - 2sinx – 1 = 0 (Phương trình bậc hai với ẩn sin x)
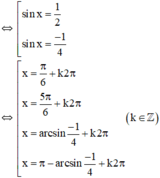
Vậy phương trình có tập nghiệm
{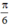 + k2π;
+ k2π; 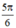 + k2π; arcsin
+ k2π; arcsin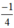 + k2π; π - arcsin
+ k2π; π - arcsin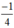 + k2π (k ∈ Z).
+ k2π (k ∈ Z).

3 cos 2 x - 2 sin x + 2 = 0 ⇔ 3 ( 1 - sin 2 x ) - 2 sin x + 2 = 0 ⇔ 3 sin 2 x + 2 sin x - 5 = 0 ⇔ ( sin x - 1 ) ( 3 sin x + 5 ) = 0 ⇔ sin x = 1 ⇔ x = π / 2 + k 2 π , k ∈ Z

\(2sinx-1=0\Leftrightarrow sinx=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Do \(x\in\left(-\dfrac{\pi}{2};\pi\right)\Rightarrow x=\left\{\dfrac{\pi}{6};\dfrac{5\pi}{6}\right\}\)

2.sin x + cos x = 1
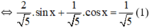
Vì 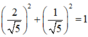 nên tồn tại α thỏa mãn
nên tồn tại α thỏa mãn 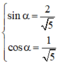
(1) trở thành:
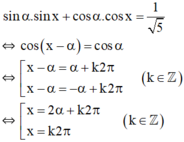
Vậy phương trình có nghiệm {k2π; 2α+k2π/k ∈ Z }
với α thỏa mãn 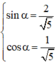

Đặt t = sin x + cos x = 2 sin x + π 4
Vì sin x + π 4 ∈ − 1 ; 1 ⇒ t ∈ − 2 ; 2
Ta có t 2 = sin x + cos x 2 = sin 2 x + cos 2 x + 2 sin x cos x ⇒ sin x cos x = t 2 − 1 2 .
Khi đó, phương trình đã cho trở thành:
t 2 − 1 2 + 2 t = 2 ⇔ t 2 + 4 t − 5 = 0 ⇔ t = 1 t = − 5 l .
Với t = 1, ta được sin x + cos x = 1 ⇔ sin x + π 4 = 1 2 ⇔ sin x + π 4 = sin π 4 .
⇔ x + π 4 = π 4 + k 2 π x + π 4 = π − π 4 + k 2 π ⇔ x = k 2 π x = π 2 + k 2 π , k ∈ ℤ
Chọn đáp án B.

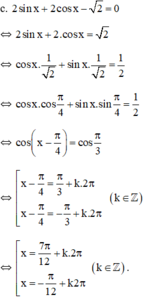
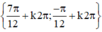 (k ∈ Z)
(k ∈ Z)
`2sin x+cosx=0`
`<=> sinx + 1/2 cosx=0`
Có: `a^2+b^2=1^2+(1/2)^2=5/4 \ne 1`
`=>` PTVN.
\(2sinx+cosx=0\)
\(\Leftrightarrow\dfrac{2}{\sqrt{5}}.sinx+\dfrac{1}{\sqrt{5}}cosx=0\)
Đặt \(cos\alpha=\dfrac{2}{\sqrt{5}}\) và \(sin\alpha=\dfrac{1}{\sqrt{5}}\) (vì \(\left(\dfrac{2}{\sqrt{5}}\right)^2+\left(\dfrac{1}{\sqrt{5}}\right)^2=1\))
pttt: \(sinx.cos\alpha+cosx.sin\alpha=0\)
\(\Leftrightarrow sin\left(x+\alpha\right)=0\)
\(\Rightarrow x=-arc.sin\alpha+k\pi\left(k\in Z\right)\)
(phải không?)