Mô tả thuật toán tính S=(1+2)+(1+2+3)+⋯+(1+2+⋯+n).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VN
3
5 tháng 1 2021
Bước 1: s←0; i←1;
Bước 2: s←s+i;
Bước 3: i←i+1;
Bước 4: Nếu i<=50 thì quay lại bước 2
Bước 5: Xuất s
Bước 6: Kết thúc
19 tháng 12 2021
#include <bits/stdc++.h>
using namespace std;
int i;
double s;
int main()
{
for (i=1; i<=49; i+=2)
s=s+1/(i*1.0);
cout<<s;
return 0;
}
7 tháng 1 2022
#include <bits/stdc++.h>
using namespace std;
int t,i;
int main()
{
t=0;
for (i=1; i<=10; i++) t=t+i;
cout<<t;
return 0;
}
DT
7 tháng 2 2022
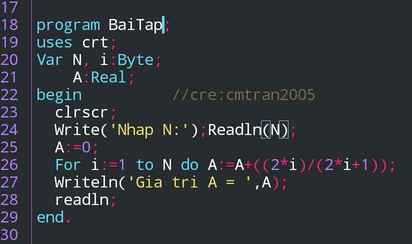
Thuật toán: B1: Nhập N;
B2: A <--- 0; i <--- 1;
B3: A <--- A + ((2*i)/(2*i+1));
B4: i <--- i + 1;
B5: Nếu i > N thì thông báo A rồi kết thúc.
B6: Quay lại bước 3;
27 tháng 12 2020
**Mô tả thuật toán S:
- Bước 1: i←0; s←0;
- Bước 2: i←i+1;
- Bước 3: s←s+i;
- Bước 4: Nếu i <= 100 thì quay lại bước 2
- Bước 5: Xuất s
- Bước 6: Kết thúc thuật toán
**Mô tả thuật toán tính P:
- Bước 1: i←0; p←1;
- Bước 2: i←i+1;
- Bước 3: p←p*i;
- Bước 4: Nếu i <= 100 thì quay lại bước 2
- Bước 5: Xuất p
- Bước 6: Kết thúc thuật toán
30 tháng 12 2021
Để đánh số trang một quyển sách dày 295 trang cần dùng bao nhiêu chữ số?
30 tháng 12 2021
a:
#include <bits/stdc++.h>
using namespace std;
long long i,n,s;
int main()
{
cin>>n;
s=0;
for (i=1; i<=n; i++) s=s+i;
cout<<s;
return 0;
}
R
24 tháng 11 2021
Câu 1 :
Tham khảo
Y tưởng : xét từng số hạng trong dãy nếu số hạng > 0 thì xếp vào một biến tổng rồi chia cho số hàng đã xếp được
Input : Dãy A gồm N số nguyên a1....aN;
Output : Trung bình cộng của các số dương;
B1 : Nhập N số nguyên a1.... aN;
B2 : TB <--- 0, dem <---- 0, i <---- 1, Tong <--- 0;
B3 : Nếu a[i] > 0 thì Tong <--- TB + a[i];
B4 : dem <--- dem + 1;
B5 : Nếu i > N thì đưa ra màn hình kết quả TB = Tong/Dem rồi kết thúc chương trình;
B 6 : i <--- i + 1 rồi quay lại B3;
Câu 2 :
Tham khảo
Ta nhận thấy rằng, bội số chung nhỏ nhất của hai số nguyên dương a, b có thể được tính theo công thức:
ab/d
trong đó d là ước chung lớn nhất của a và b.
Bởi vậy:
Nên viết hàm để tính bội chung nhỏ nhất của hai số nguyên dương vì chương trình con cần trả ra một giá trị;
- Hàm tính bội chung nhỏ nhất của hai số nguyên dương a, b cần sử dụng hàm tính ước chung lớn nhất của a và b.
- Hàm tính ước chung lớn nhất của hai số nguyên dương a, b:
function ucln (a, b: integer): integer;
var r: integer;
begin
while b>0 do begin
r: = a mod b ,a : = b ; b:= r; end; ucln:= a; and;
- Hàm tính bội chung nhỏ nhất của hai số nguyên dương a, b:
ADVERTISING Video Player is loading.This is a modal window.
The media could not be loaded, either because the server or network failed or because the format is not supported.
lunction bcnn(a, b: integer): integer;
begin
bcnn:= a*b div ucln(a, b);
end;
Khi đó, chương trình con tính bội số chung nhỏ nhất của hai số nguyên dương a, b như sau:
program bai4_chuong6;
use crt ;
vai
X y: integer;
function ucln(a, b: integer): integer;
var r: integer;
begin
while b>0 do begin
r:= a mod b; a: = b ,b:= r;
end; ucln:= a;
end;
txnction bcnn(a, b: integer): integer;
begin
bcnn:= a*b div ucln(a, b);
end;
Begin
clrscr;
writeln('Nhap vao hai so can tim BCNN');
write ('x=') , readln(x); write ('y=') , readln(y);
writeln('bcnn cua hai so',x:4,'va',y:4,'la',bcnn(a,b)
readln
End.
Câu 3 : chịu
2 tháng 1 2022
c:
#include <bits/stdc++.h>
using namespace std;
long long ln,i,n,x;
int main()
{
cin>>n;
ln=LLONG_MIN;
for (i=1; i<=n; i++)
{
cin>>x;
ln=max(ln,x);
}
cout<<ln;
return 0;
}
P
1
Thuật toán tính tổng \(S = \left(\right. 1 + 2 \left.\right) + \left(\right. 1 + 2 + 3 \left.\right) + \hdots + \left(\right. 1 + 2 + \hdots + n \left.\right)\) có thể mô tả như sau:
Mô tả thuật toán
Công thức rút gọn
Tổng \(S\) có thể được tính nhanh bằng công thức:
\(S = \sum_{i = 1}^{n} \frac{i \left(\right. i + 1 \left.\right)}{2} = \frac{1}{2} \sum_{i = 1}^{n} \left(\right. i^{2} + i \left.\right) = \frac{1}{2} \left(\right. \sum_{i = 1}^{n} i^{2} + \sum_{i = 1}^{n} i \left.\right)\)Với:
\(\sum_{i = 1}^{n} i = \frac{n \left(\right. n + 1 \left.\right)}{2}\) \(\sum_{i = 1}^{n} i^{2} = \frac{n \left(\right. n + 1 \left.\right) \left(\right. 2 n + 1 \left.\right)}{6}\)Thay vào ta có:
\(S = \frac{1}{2} \left(\right. \frac{n \left(\right. n + 1 \left.\right) \left(\right. 2 n + 1 \left.\right)}{6} + \frac{n \left(\right. n + 1 \left.\right)}{2} \left.\right) = \frac{n \left(\right. n + 1 \left.\right) \left(\right. n + 2 \left.\right)}{6}\)Tóm tắt thuật toán theo bước
Ví dụ
Nhưng theo biểu thức đề bài (có thể bắt đầu từ \(i = 1\) với \(\left(\right. 1 \left.\right)\) hoặc \(\left(\right. 1 + 2 \left.\right)\) tùy cách hiểu), ví dụ tại nguồn có kết quả \(S = 10\) khi \(n = 3\) (có tính thêm \(1\) ở đầu), nên cần lưu ý cách tính tổng từng phần6.
Thuật toán này được mô tả chi tiết và có ví dụ mi