Bài 4. (2,5 điểm) Cho $(O; R)$ đường kính $AB$. Bán kính $CO$ vuông góc với $AB$, $M$ là điểm bất kì trên cung nhỏ $AC$ ($M$ khác $A$ và $C$), $MB$ cắt $AC$ tại $H$. Gọi $K$ là hình chiếu của $H$ trên $AB$.a) Chứng minh bốn điểm $C$, $B$, $H$, $K$ cùng thuộc một đường tròn.b) Chứng minh $CA$ là phân giác góc $MCK$.c) Kẻ $Ax$ là tiếp tuyến của nửa đường tròn tại $A$. Lấy $P \in Ax$ sao cho $\dfrac{AP. MB}{MA} =...
Đọc tiếp
Bài 4. (2,5 điểm) Cho $(O; R)$ đường kính $AB$. Bán kính $CO$ vuông góc với $AB$, $M$ là điểm bất kì trên cung nhỏ $AC$ ($M$ khác $A$ và $C$), $MB$ cắt $AC$ tại $H$. Gọi $K$ là hình chiếu của $H$ trên $AB$.
a) Chứng minh bốn điểm $C$, $B$, $H$, $K$ cùng thuộc một đường tròn.
b) Chứng minh $CA$ là phân giác góc $MCK$.
c) Kẻ $Ax$ là tiếp tuyến của nửa đường tròn tại $A$. Lấy $P \in Ax$ sao cho $\dfrac{AP. MB}{MA} = R$
Chứng minh $PB$ đi qua trung điểm của đoạn thẳng $HK$.
BC
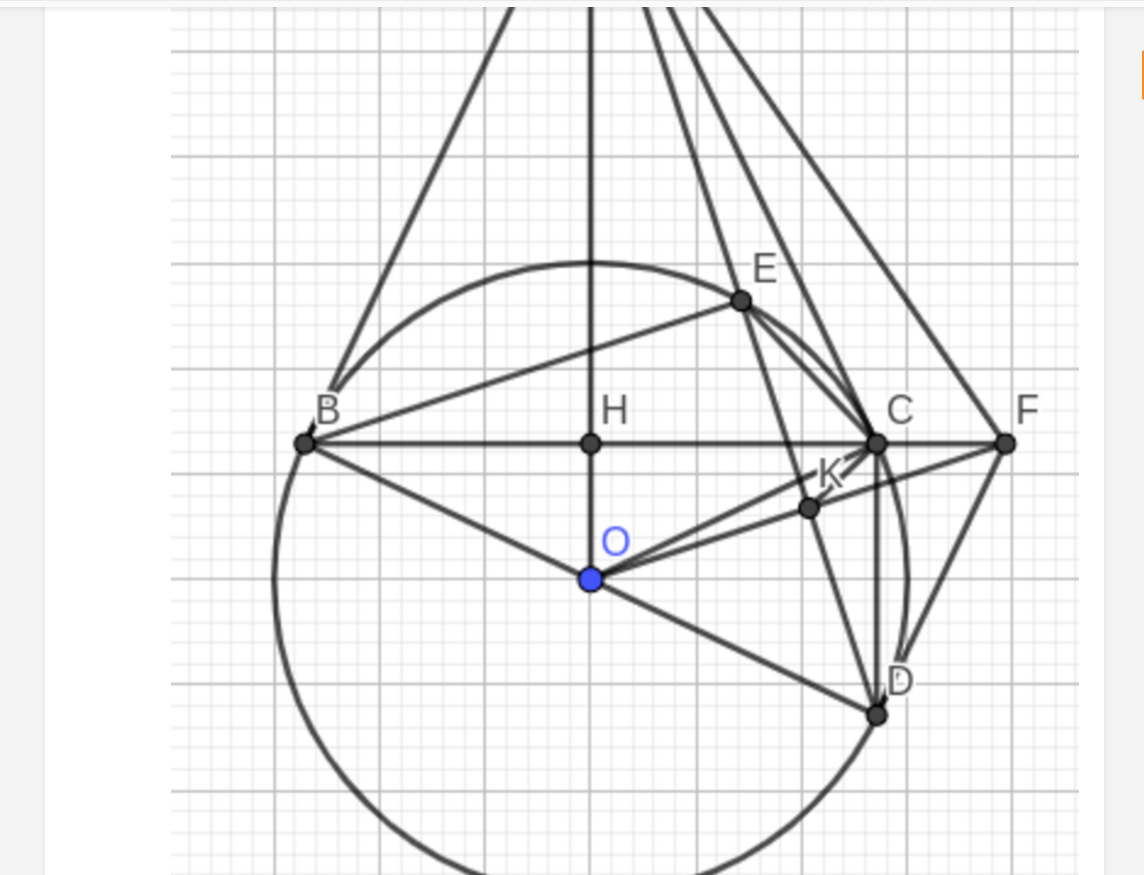
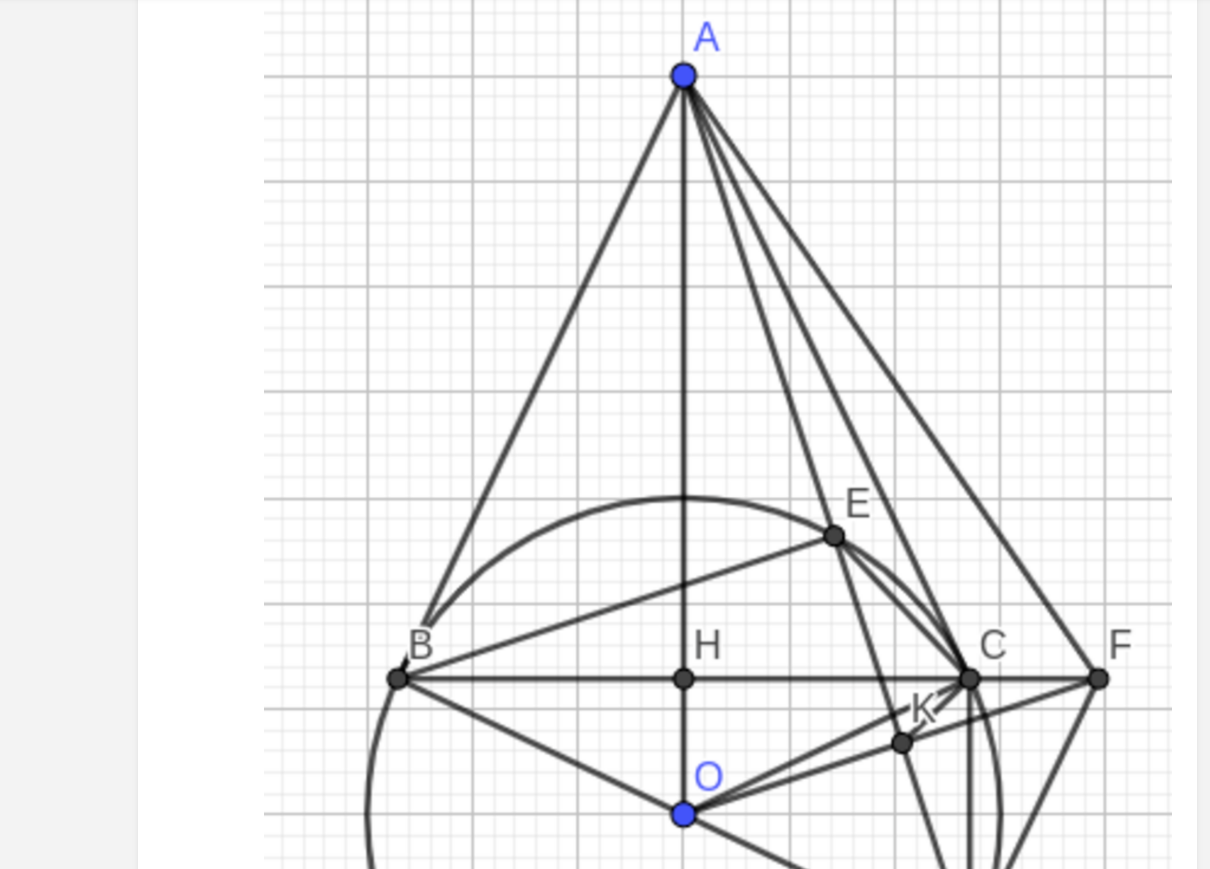
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét tứ giác BCHK có \(\widehat{BCH}+\widehat{BKH}=90^0+90^0=180^0\)
nên BCHK là tứ giác nội tiếp
=>B,C,H,K cùng thuộc một đường tròn
b: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
Xét tứ giác AMHK có \(\widehat{AMH}+\widehat{AKH}=90^0+90^0=180^0\)
nên AMHK là tứ giác nội tiếp
ta có: BCHK nội tiếp
=>\(\widehat{KCH}=\widehat{KBH}\)
=>\(\widehat{KCA}=\widehat{MBA}\)
mà \(\widehat{MBA}=\widehat{MCA}\)
nên \(\widehat{KCA}=\widehat{MCA}\)
=>CA là phân giác của góc MCK