Các bài toán tổng hiệu nâng cao
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A
1
16 tháng 7 2016
Hiện nay tổng số tuổi của 3 bố con Hồng và Huệ là 47 tuổi. Cách đây 2 năm tuổi bố hơn tuổi của Hồng và Huệ là 27 tuổi. Hỏi hiện nay mỗi người bao nhiêu tuổi ? biết rằng Hồng hơn Huệ 5 tuổi
5 tháng 5 2021
1. Ta có 3/4=6/8 2/5=6/12
theo đề bài 6/8 st1 = 6/12 st2
Hay 1/8 số thứ 1 = 1/12 st2
Coi st1 là 8 phần = nhau thì st2 là 12 phần như thế
Ta có sơ đồ : tự vẽ
St1 là : 230:(8+12)*8=92
St2 là : 230-92 =138
Đ/s
9 tháng 3 2016
Bài giải: Ta đặt A = 1 + 2 + 3 + 4 + 5 + ... + 49 + 50. Dãy số tự nhiên liên tiếp từ 1 đến 50 có 50 số, trong đó số các số lẻ bằng số các số
chẵn nên có 50 : 2 = 25 (số lẻ). Vậy A là một số lẻ. Gọi a và b là hai số bất kì của A, khi thay tổng a + b bằng hiệu a - b thì A giảm đi: (a + b) -
(a - b) = 2 x b tức là giảm đi một số chẵn. Hiệu của một số lẻ và một số chẵn luôn là một số lẻ nên sau mỗi lần thay, tổng mới vẫn là một số
lẻ. Vì vậy không bao giờ nhận được kết quả là 0.
9 tháng 3 2016
Bài giải: Ta đặt A = 1 + 2 + 3 + 4 + 5 + ... + 49 + 50. Dãy số tự nhiên liên tiếp từ 1 đến 50 có 50 số, trong đó số các số lẻ bằng số các số
chẵn nên có 50 : 2 = 25 (số lẻ). Vậy A là một số lẻ. Gọi a và b là hai số bất kì của A, khi thay tổng a + b bằng hiệu a - b thì A giảm đi: (a + b) -
(a - b) = 2 x b tức là giảm đi một số chẵn. Hiệu của một số lẻ và một số chẵn luôn là một số lẻ nên sau mỗi lần thay, tổng mới vẫn là một số
lẻ. Vì vậy không bao giờ nhận được kết quả là 0.
Z
1
6 tháng 1 2022
\(\text{Ta có:}\)
\(y^2=xz\Leftrightarrow\dfrac{x}{y}=\dfrac{y}{z}\left(1\right)\)
\(z^2=yt\Leftrightarrow\dfrac{x}{y}=\dfrac{t}{x}\left(2\right)\)
\(\text{Từ (1) và (2)}\Leftrightarrow\dfrac{x}{y}=\dfrac{y}{z}=\dfrac{t}{x}\)
\(\Leftrightarrow\dfrac{x^3}{y^3}=\dfrac{y^3}{z^3}=\dfrac{t^3}{x^3}\)
\(\text{Áp dụng tính chất dãy tỉ số bằng nhau:}\)
\(\dfrac{x^3}{y^3}=\dfrac{y^3}{z^3}=\dfrac{t^3}{x^3}=\dfrac{x^3+y^3+t^3}{y^3+z^3+x^3}\)
\(\Leftrightarrow\dfrac{x^3}{t^3}=\dfrac{y^3+z^3+x^3}{y^3+z^3+x^3}\left(đpcm\right)\)
NH
0
VH
1
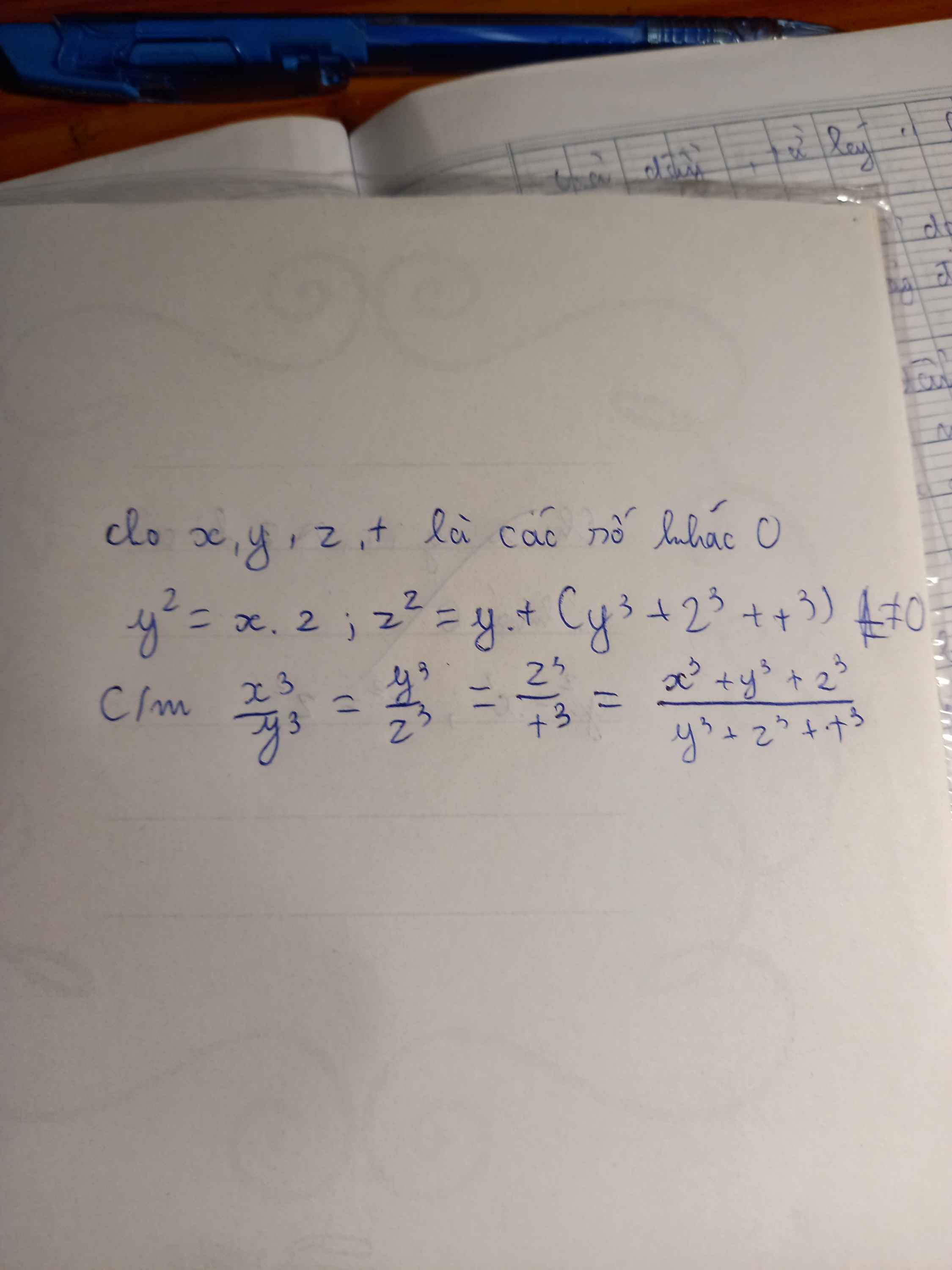
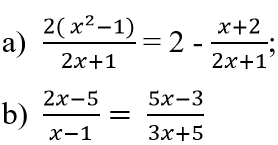
cần ji hả bạn
Olm chào em, trong khóa học của Olm có tất các dạng bài toán nâng cao, em có thể luyện để nâng cao kiến thức em nhé. Đối với những tài khoản không phải vip của Olm thì không thể luyện lại bài tập, không thể xem hết bài giảng, đang xem sẽ bị dừng, không xem được đáp án, không nộp được bài, em nhé. Trừ khi cô giáo giao lại bài đó cho em làm lại thì được.
Để sử dụng toàn bộ học liệu của Olm thì em vui lòng kích hoạt vip olm. Quyền lợi của Olm vip là sử dụng toàn bộ học liệu của Olm từ lớp 1 đến lớp 12. Học và luyện không giới hạn bài giảng bài tập của Olm. Cùng hàng triệu đề thi thông minh, ngân hàng câu hỏi. Hỏi bài không giới hạn trên diễn đàn hỏi đáp, tương tác với giáo viên qua zalo.